A liquid kept in a cylindrical vessel of radius 0.3 m is rotated with a speed 2 r.p.s. The difference in the height of the liquid at the centre of the vessel and at it's sides it
0.01 m
0.02 m
0.04 m
0.8 m
The correct Answer is:4
To solve the problem of finding the difference in height of the liquid at the center of a cylindrical vessel and at its sides when the vessel is rotated, we can follow these steps:
1. Identify Given Values:
- Radius of the cylindrical vessel, R=0.3m
- Speed of rotation, n=2r.p.s
2. Convert Revolutions per Second to Angular Velocity:
- The angular velocity ω in radians per second is given by:
ω=2πn=2π×2=4πrad/s
3. Calculate the Linear Velocity at the Radius:
- The linear velocity V at the edge of the vessel is given by:
V=Rω=0.3×4π=1.2πm/s
4. Apply Bernoulli's Equation:
- According to Bernoulli's principle, we can relate the pressure difference between the center and the side of the liquid. The difference in height H can be calculated using:
H=V22g
- Where g is the acceleration due to gravity (approximately 10m/s2).
5. Substitute the Values:
- First, calculate V2:
V2=(1.2π)2=1.44π2m2/s2
- Now, substitute into the height equation:
H=1.44π22×10=1.44π220=0.072π2m
6. Calculate the Numerical Value:
- Using π≈3.14:
H≈0.072×(3.14)2≈0.072×9.8596≈0.710m
7. Final Result:
- The difference in height of the liquid at the center and at the sides of the vessel is approximately:
H≈0.71m
Conclusion:
The difference in the height of the liquid at the center of the vessel and at its sides is approximately 0.71 meters.
- Radius of the cylindrical vessel, R=0.3m
- Speed of rotation, n=2r.p.s
- The angular velocity ω in radians per second is given by:
ω=2πn=2π×2=4πrad/s
- The linear velocity V at the edge of the vessel is given by:
V=Rω=0.3×4π=1.2πm/s
- According to Bernoulli's principle, we can relate the pressure difference between the center and the side of the liquid. The difference in height H can be calculated using:
H=V22g
- Where g is the acceleration due to gravity (approximately 10m/s2).
- First, calculate V2:
V2=(1.2π)2=1.44π2m2/s2
- Now, substitute into the height equation:
H=1.44π22×10=1.44π220=0.072π2m
- Using π≈3.14:
H≈0.072×(3.14)2≈0.072×9.8596≈0.710m
- The difference in height of the liquid at the center and at the sides of the vessel is approximately:
H≈0.71m
The difference in the height of the liquid at the center of the vessel and at its sides is approximately 0.71 meters.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Level 2 (H.W)
Explore 39 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Illustration
Explore 62 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:integer Type Questions
Explore 25 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
The product of the numbers 5623 and 6 in the scale of eight is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View Solution
Knowledge Check
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
A8cmB2cmC40cmD4cmA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
Ah=2π2n2r2gBh=4π2n2r2gCh=π2r2n2gDh=π2r2n2gA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
Arω2gBr2ω22gC√2grωDω22gr2
A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
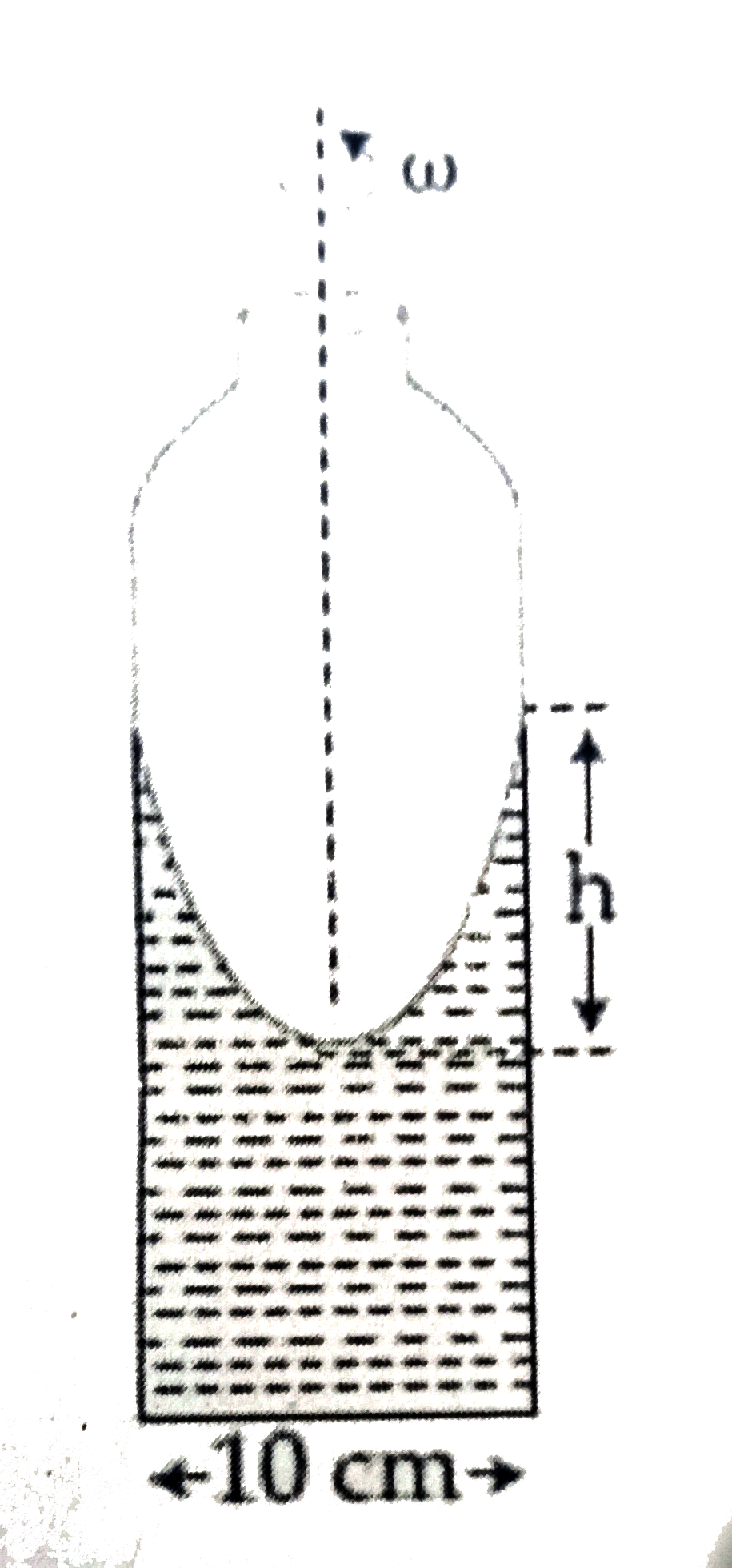
View SolutionA cylinder vessel of radius 10 cm containing a liquid is rotating about a vertical axis through the centre of circular base. The vessel is rotating with angular frequency 10 rad/s. Find the difference of the heights of liquid at centre of vessel and edge.
View SolutionFind the capacity of a cylindrical vessel, whose radius is 3m. and height 7m.
View SolutionA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
View SolutionA cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
View Solution

