A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
h=2π2n2r2g
h=4π2n2r2g
h=π2r2n2g
h=π2r2n2g
The correct Answer is:A
When the cylindrical vessel rotats the velocity at the sides is higher. Hence pressure at the sides is lower.

Equation of sruface liquid is y=ω2x22g
Here ω=2πn
x=R
y=h
h=(2πn)2(R2)2g=2π2n2r2g
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionThe product of the numbers 5623 and 6 in the scale of eight is
View Solution
Knowledge Check
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
A8cmB2cmC40cmD4cmA liquid is kept in a cylindrical jar, which is rotated about the cylindrical axis. The liquid rises at its sides. The radius of the jar is r and speed of rotation is Ω the difference in height at the centre and the sides of the jar is
Ar2ω2gBr2ω22gCgr2ω2D2gr2ω2A liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
Arω2gBr2ω22gC√2grωDω22gr2
A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
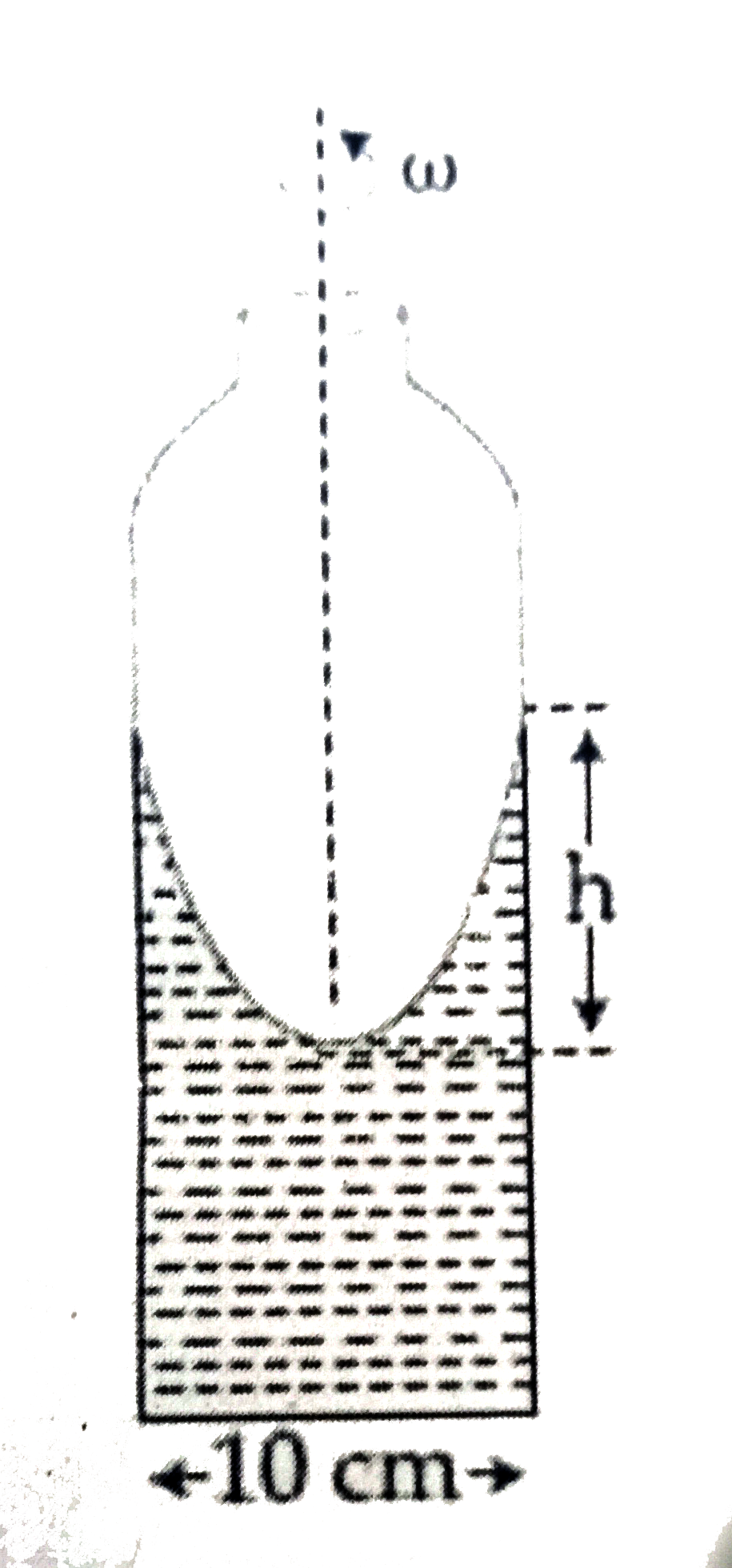
View SolutionA long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
View SolutionA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
View SolutionA long cylinderical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis. The liquid rises up near the wall. If the radius of vessel is 5cm and its rotational speed is 2 rotatins per second, then the difference in the heights between the centre and the sides, in cm. will be :
View SolutionA long cylinderical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis. The liquid rises up near the wall. If the radius of vessel is 5cm and its rotational speed is 2 rotatins per second, then the difference in the heights between the centre and the sides, in cm. will be :
View Solution

