Three identical blocks each of mass m=1kg and volume 3×10−4m3 are suspended by massless strings from a support as shown. Underneath are three identical containers containing the same amount of water that are placed over the scales. In Fig. (a), the block is completely out of the water, in Fig. (b), the block is completely submerged but not touching the beaker and in Fig. (c), the block rests on the bottom of the beaker. The scale in Fig (a) reads 14N.
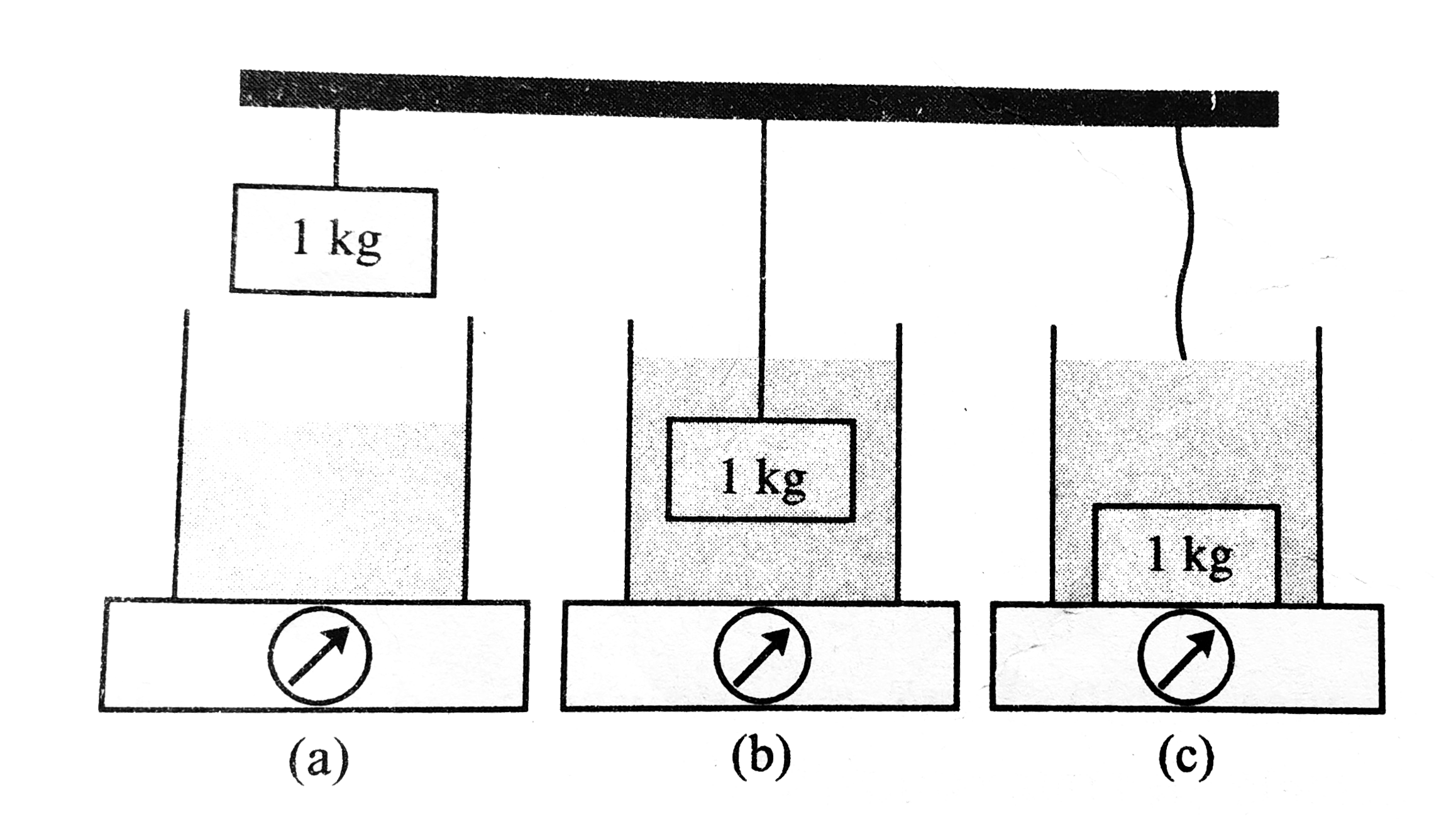
The tension in the string in (b) is 10N.
The tension in the string in (b) is 7N.
The reading of the scale in (b) is 17N
The reading of the scale in (c) is 24N.
The correct Answer is:B, C, D
Density of the block =13×10−4kg/m3=103×103kg/m3
Buoyant force B=3×10−4×103×g=3N
∴TB=10=3=7N
Reading of B=14+3=17N
Reading of C=[14+(10−3)+3]N=24N
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Three identical blocks each of mass M are along a frictionless table and a force F is acting as shown. Which of the following statements is false ?
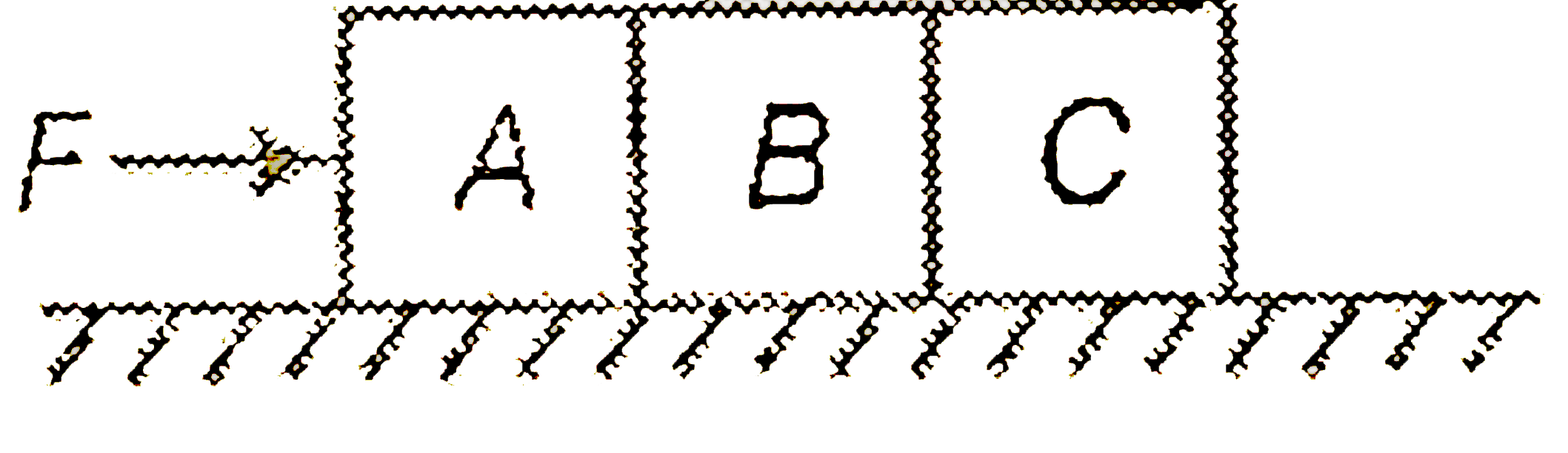
View SolutionA block of bras of mass 0.5 kg and density 8×103kg/m3 is suspended from a string. What will be the tension in the string if the block is completely immersed in water? (g=10ms−2)
View Solution
Knowledge Check
A block of aluminium of mass 1kg and volume 3.6×10−4m3 is suspended from a string and then completely immersed in a container of water. The decrease in tension in the string after immersion is.
A9.8NB6.2NC3.6ND1.0NIn fig. a small block is kept on m. then
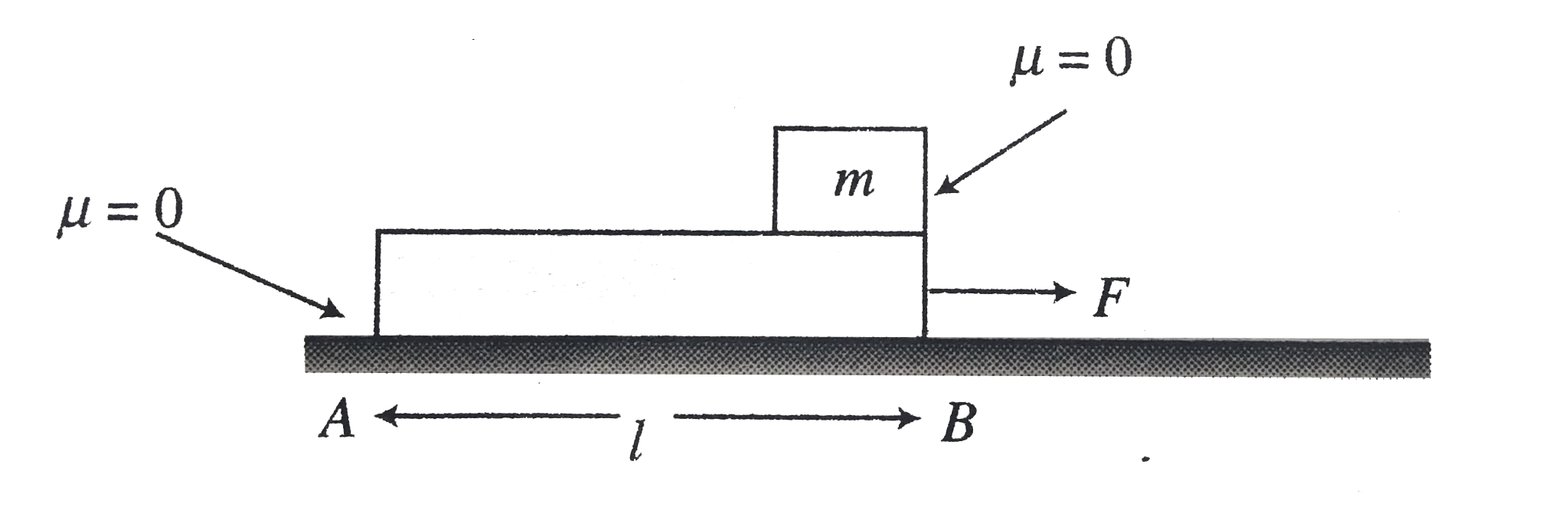 AThe acceleration of m w.r.t. ground is F/m.BThe acceleration of m w.r.t ground is zero.CThe time taken by m to separted from M is √2lmF.DThe time taken by m to separted from M is √2lMF.
AThe acceleration of m w.r.t. ground is F/m.BThe acceleration of m w.r.t ground is zero.CThe time taken by m to separted from M is √2lmF.DThe time taken by m to separted from M is √2lMF.A block of aluminium of mass 1 kg and volume 3.6×10−4m3 is suspended from a string and then completely immmersed in a container of water. The decreases in tension in the string after immersion is (use g=10ms−2)
A9.8 NB6.2 NC3.6 ND1.0 N

Three blocks A, B and C havig masses m kg, 2kg and 3 kg are attached by massless strings and ideal pulleys as shown in the figure. When the system is realeased from rest if the block A remains stationary. the mass of block A is
View SolutionThree identical blocks, each having a mass m are pushed by a force F on the Frictionless table as shown in figure.
What is the net force on the block A?

View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionA block of mass 4 kg and volume 5×10−4m3 is suspended by a spring balance in a lift which is accelerating. The apparent weight shown by the spring balance is 3 kg. Now the block is immersed in water in kg shown by the spring balance is
View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-

View Solution

