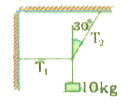
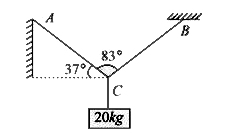
A block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

Method I: Considering equilibrium of each part of system
The whole system is in equilibrium, therefore, for each part . From the free body diagram of block C, .
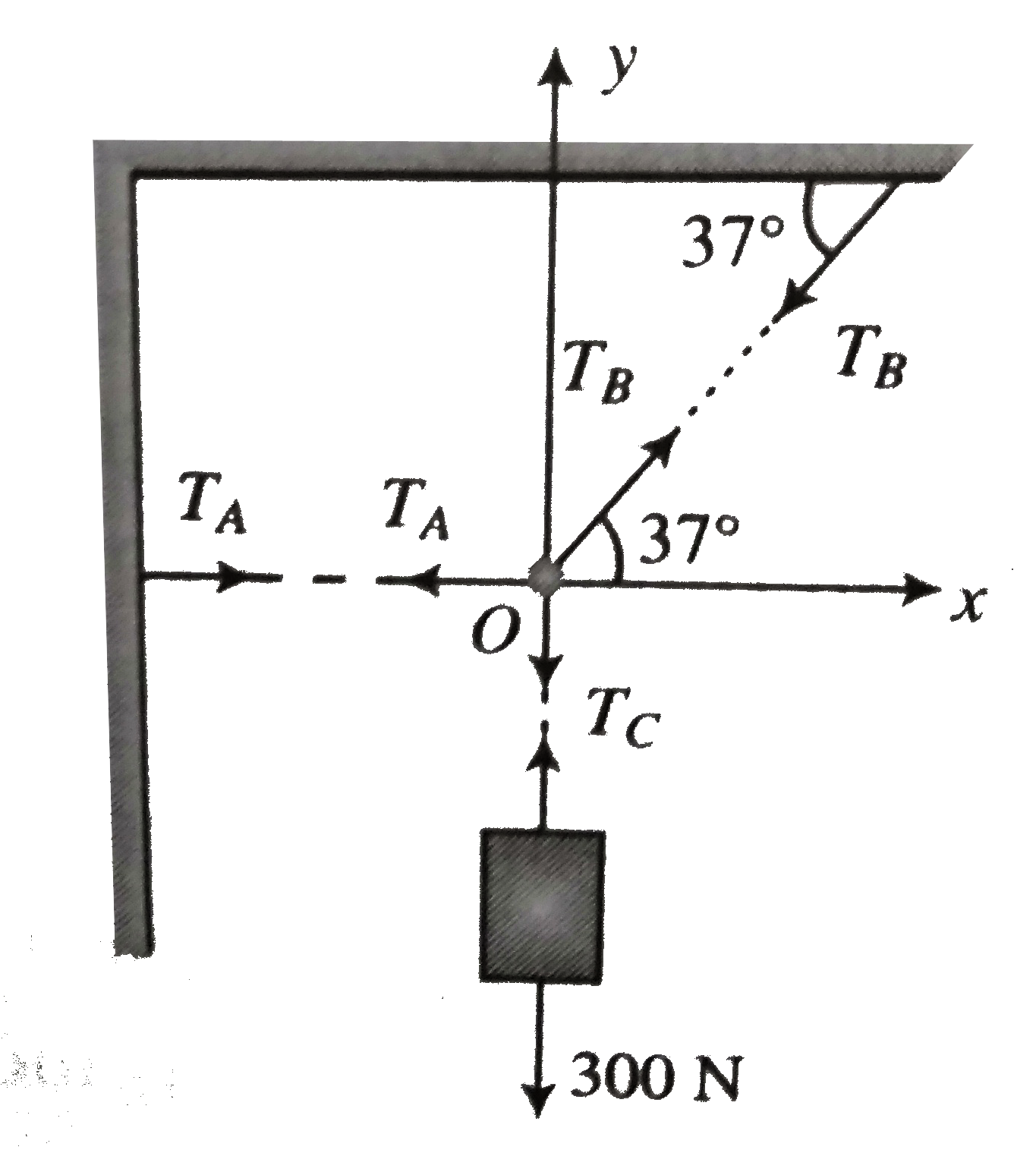
Now consider the equilibrium of point O,
...(i)
and ...(ii)
From Eq.(i), we get
.
Method II: Using Lami's theoram
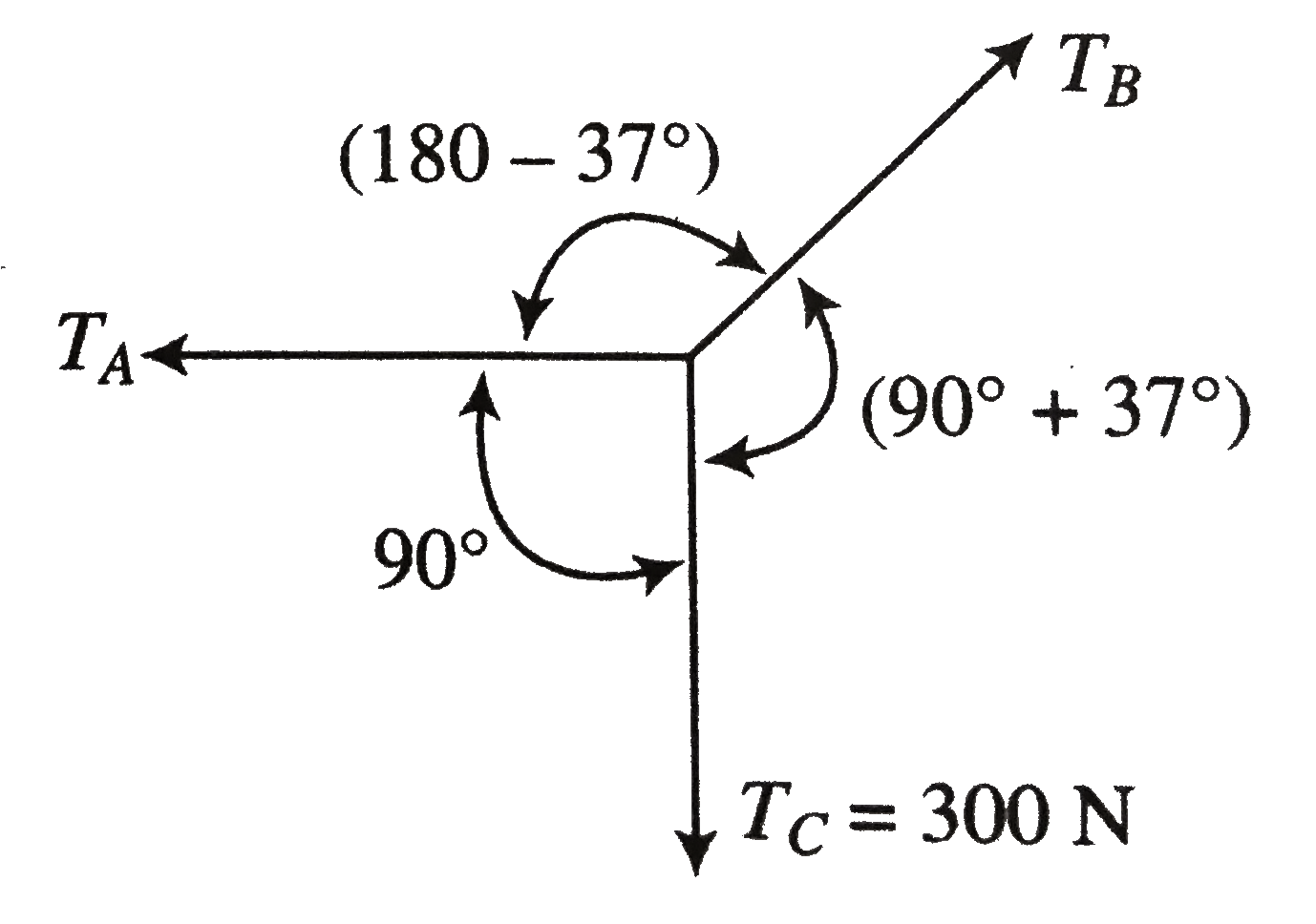
By Lami's theoram, we have
But
and
.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Solved Examples
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.1
Explore 11 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
Knowledge Check
A block of mass 10 kg is suspended by three strings as shown in figure . Tension T2 is
 A100NB100√3NC√3×100ND50√3N
A100NB100√3NC√3×100ND50√3NA block of mass 3m is suspended by a meter scale rod of mass m as shown in figure. If the tension in the string A is equal to kmg in equilibrium, then value of k will be
 A43955B43926C43895D43835
A43955B43926C43895D43835A block of weight W is supported by three strings as shown in figure. Which of the following relations is true for tension in the string ? (Here, T1,T2 and T3 are the tension in the strings A,B and C respectively)
 AT1=T2BT1=T3CT2=T3DT1=T2=T3
AT1=T2BT1=T3CT2=T3DT1=T2=T3
A block of mass 20kg is balanced by three strings A, B & C as shown in figure. Ratio of tensions in strings AC and BC(TA/TB) is
View SolutionA block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
View SolutionA block of mass 6 kg is kept in equilibrium with the help of strings as shown in figure. The tension in string PQ is (g = 10 m/s2)
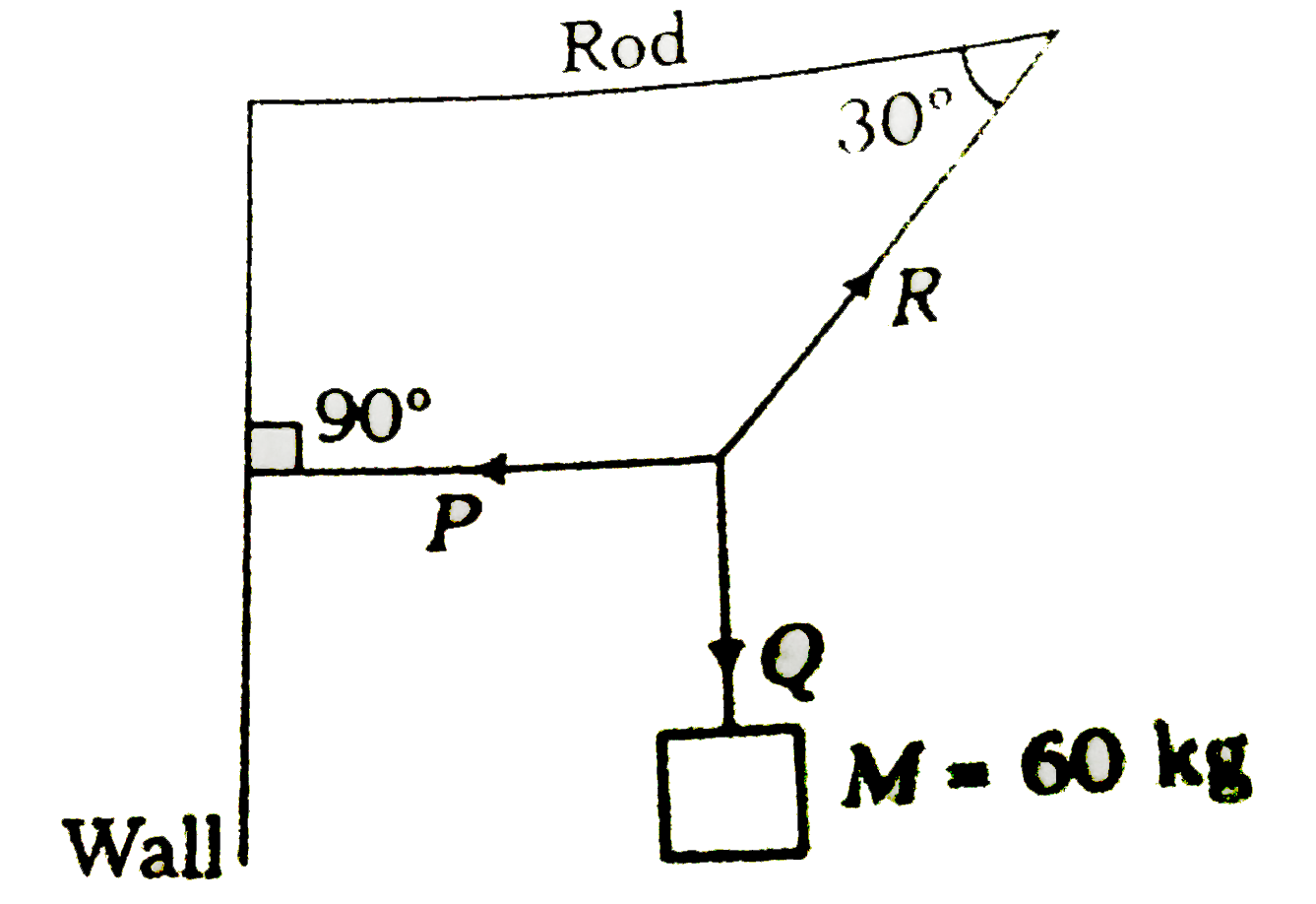
View SolutionA body of mass 60 kg suspended by means of three strings, P, Q and R as shown in the figure is in equlibrium. The tension in the string P is
View SolutionA 100 kg block is suspended with the help of three strings A, B and C. The tension in the string A is

View Solution