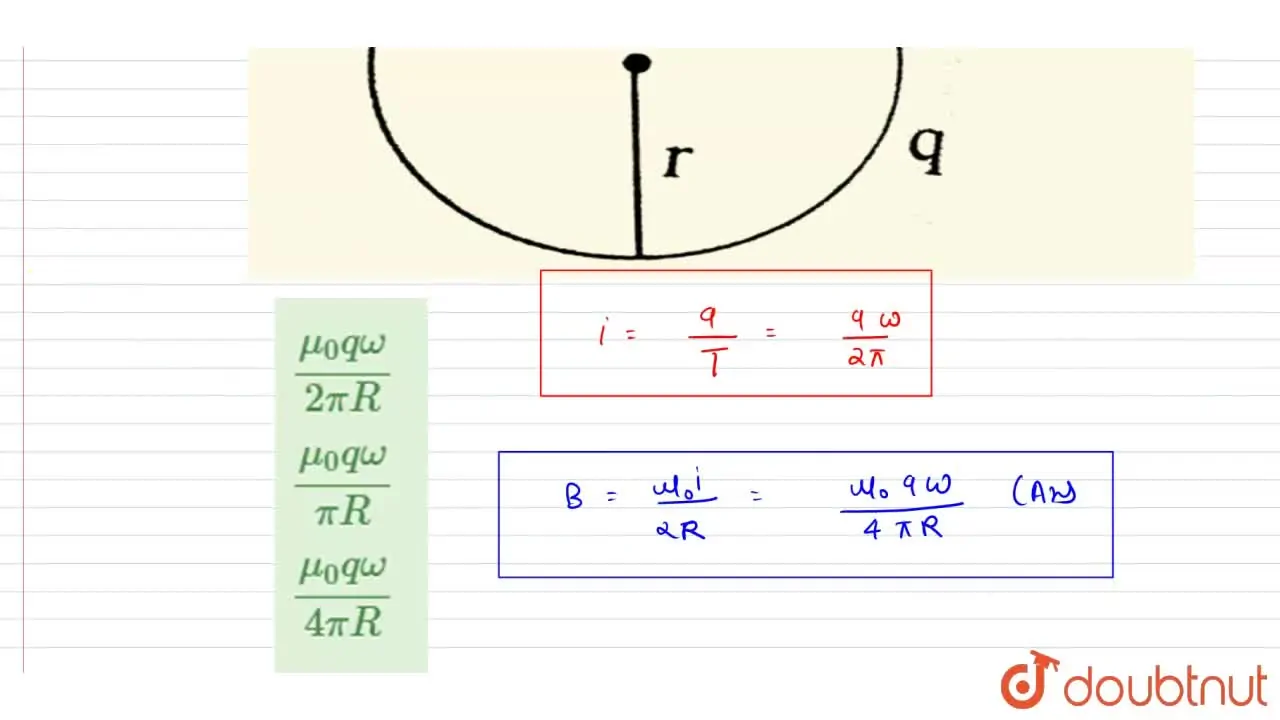
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

μ0qω2πR
μ0qωπR
μ0qω4πR
zero
The correct Answer is:C
Step by step video & image solution for A conducting ring of radius r having charge q is rotating with angular velocity omega about its axes. Find the magnetic field at the centre of the ring. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.
 View Solution
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.View SolutionThere is a ring of radius r having linear charge density λ and rotating with a uniform angular velocity ω. the magnetic field produced by this ring at its own centre would be
View SolutionA conducting ring of radius 'r' is rolling without slipping with a constant angular velocity ω (figure). If the magnetic field strengh is B and is directed into the page the emf induced across PQ is
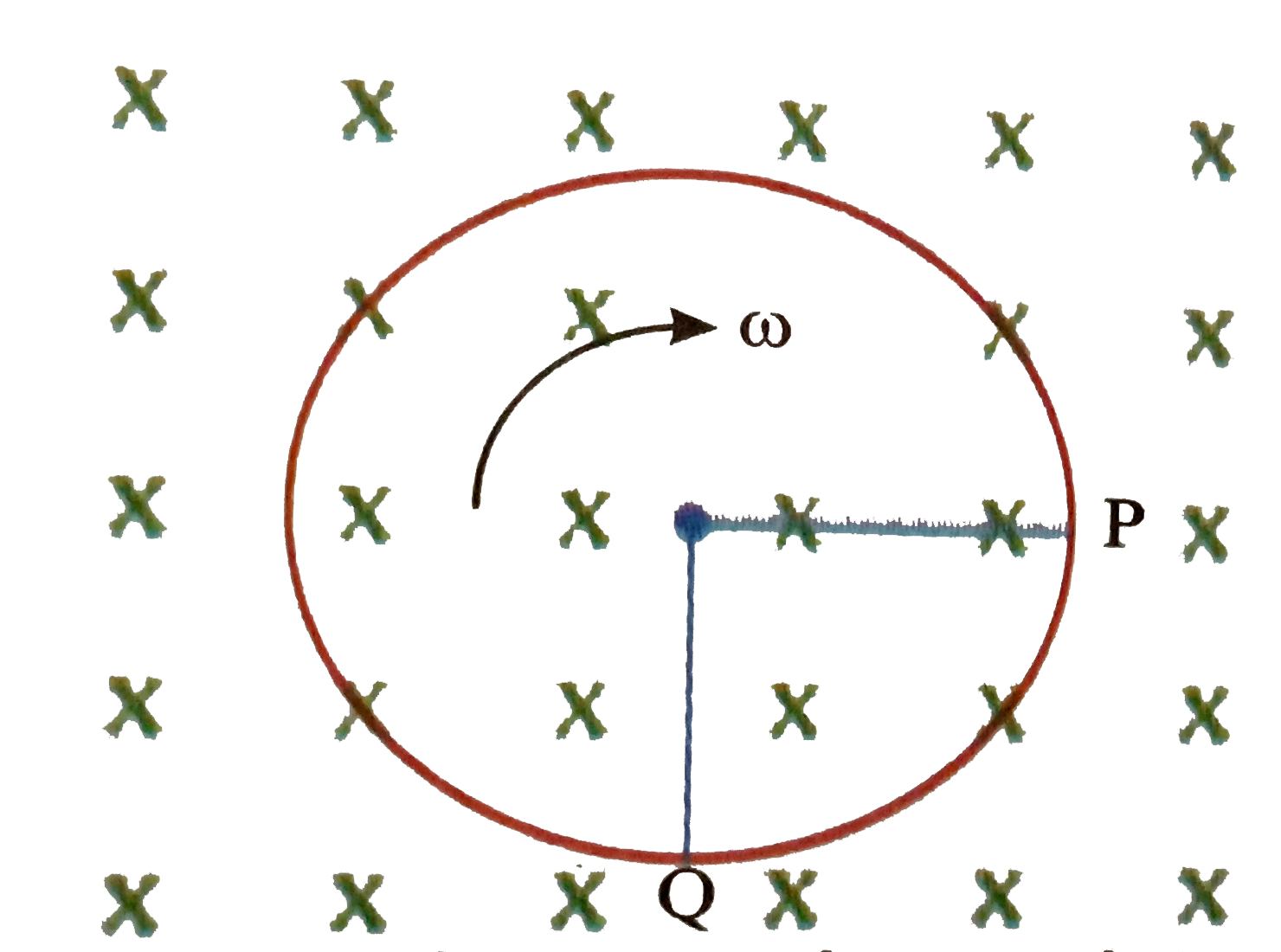 View Solution
View SolutionA thin uniform ring of radius R carrying charge q and mass m rotates about its axis with angular velocity ω. Find the ratio of its magnetic moment and angular momentum.
View SolutionA conducting circular loop of radius r is rotated about its diameter at a constant angular velocity ω in a magnetic field B perpendicular to the axis of rotation. In what position of the loop is the induced emf zero?
View SolutionConsider two uniformaly charged concentric and coaxial rings of radii R and 2R. Total charge on inner ring is Q1 and that on outer ring is Q2. Both rings are revolving in same sence with same angular velocity about its axis. If net magnetic induction at a distance R feom the centre of the rings, on axis of rings is zero then Q1Q2 is :
View SolutionA uniformly charged disc of radius r and having charge q rotates with constant angular velocity ω. The magnetic dipole moment of this disc is 1nqωr2. Find the value of n.
View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View Solution