Using Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
Considering the whole line charge to be made of symmetrically situated length elements, each of length dI, it is clear from the figure shown that, the resultant field will be directed perpendicular to the line charge as shown-

To find magnitude
Now considering a cylindrical gaussian surface of radius r and length l , passing through point p , as shown
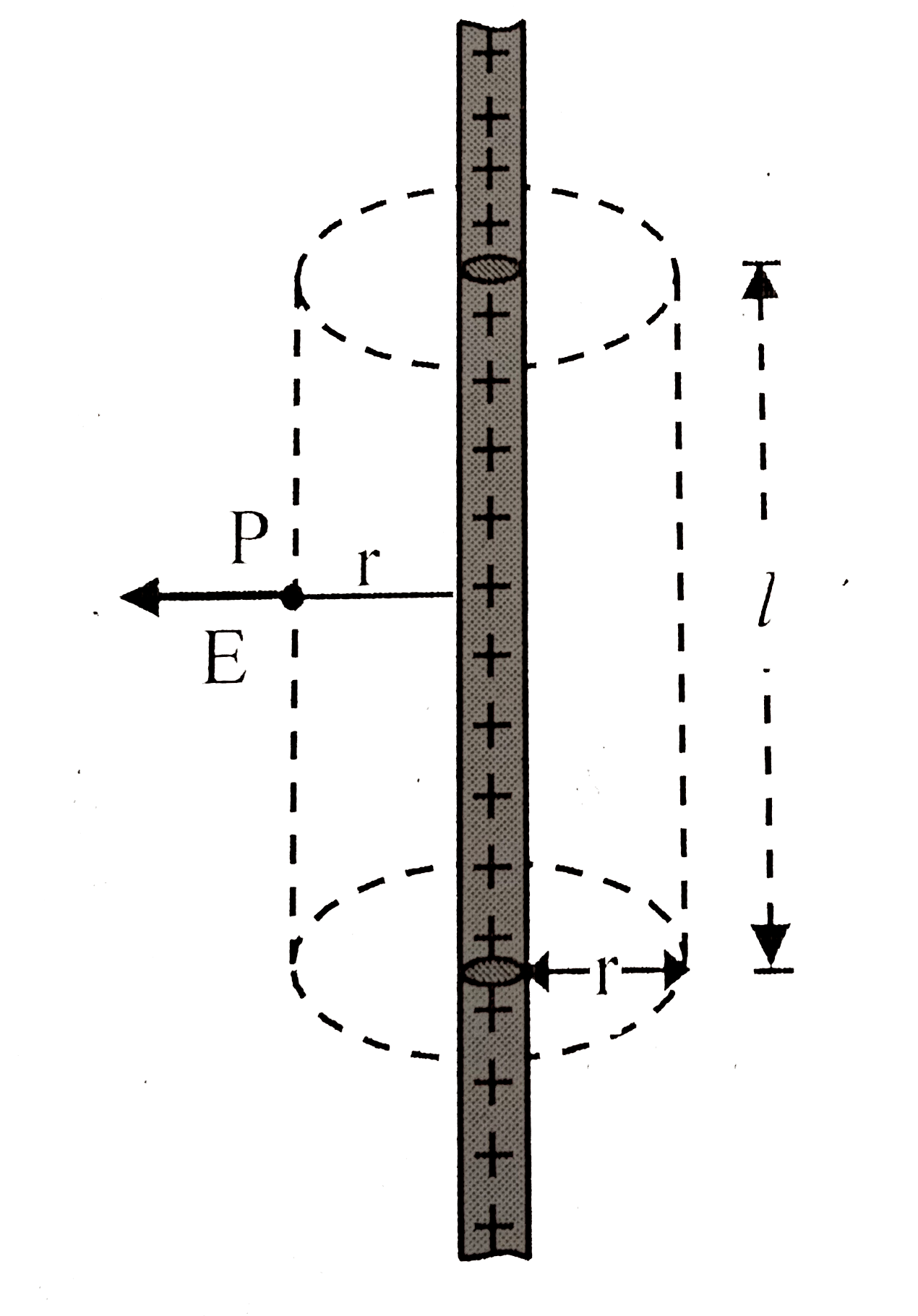
Flux through the Gaussian Surface= Flux through the curved Cylindrical part Φ=E×2πrl .....(1) , But according to Gauss’ law [Φ=Σqε0]
net electric flux emerging from cylindrical surface is [Φ=λlε0] ....(2) [ The surface includes charge equal to λl ]
Now , eliminatingΦ–– from equation (1) & (2), we get
E×2πrl=λε0 or E=λ2πε0r=2kλr
And in vector form →E=2kλr2→r
Topper's Solved these Questions
Similar Questions
Using Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
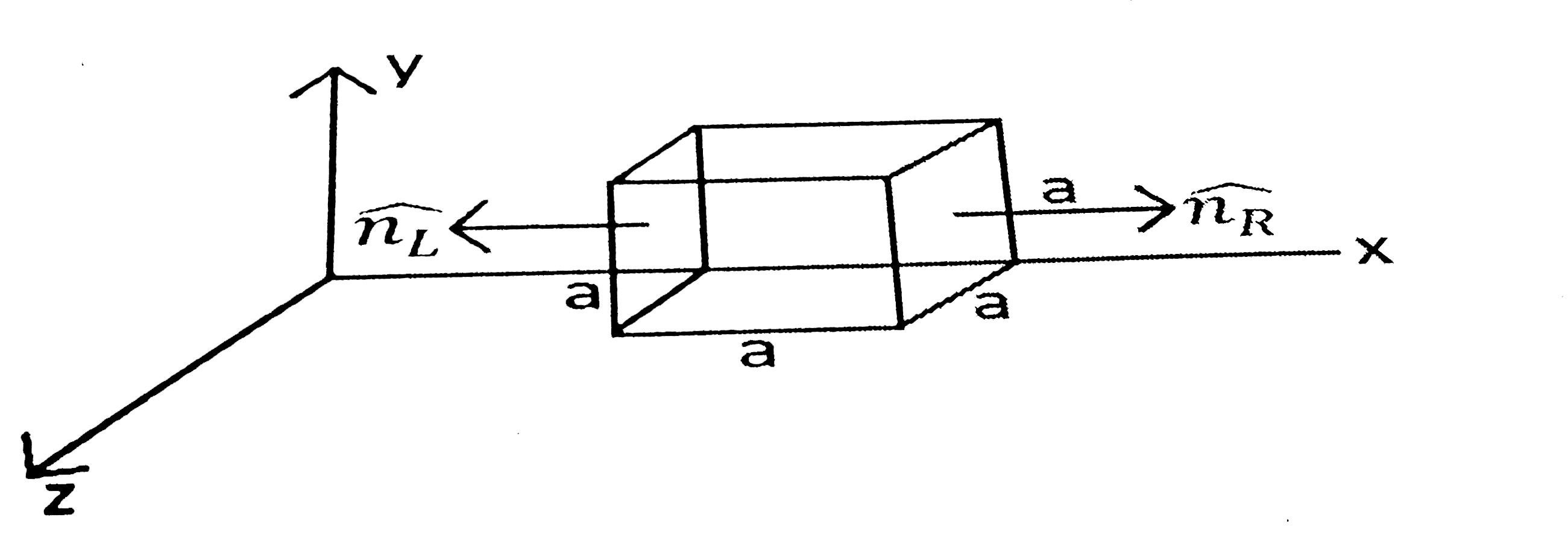
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
 View Solution
View SolutionAnswer the following:
State Gauss' law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire.View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.View SolutionState Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionAnswer the following:
(a) State Gauss' law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View Solution(a) Use Gauss's law to derive the expression for the electric filed (→E) due to straight uniformaly charges infinite line of charges density λC/m.
(b) Draw a graph to show the variation of E with perpendicular from the line of charge.
(c) Find the work done in brining a charge q from prependicular distance r1 to r2(r2>r1).View SolutionUse Gauss's law to derive the expression for the electric field between two uniformly charged large parallel sheets with surface charge densities σ and −σ respectively.
View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View Solution
