Using Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
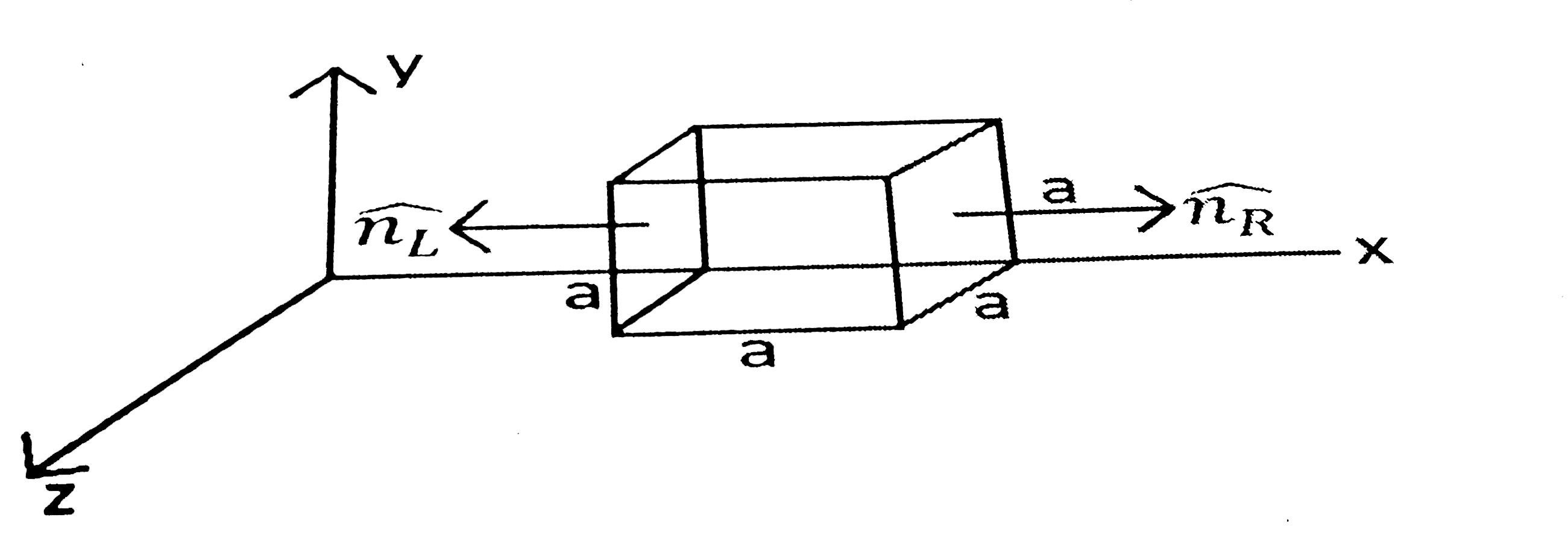
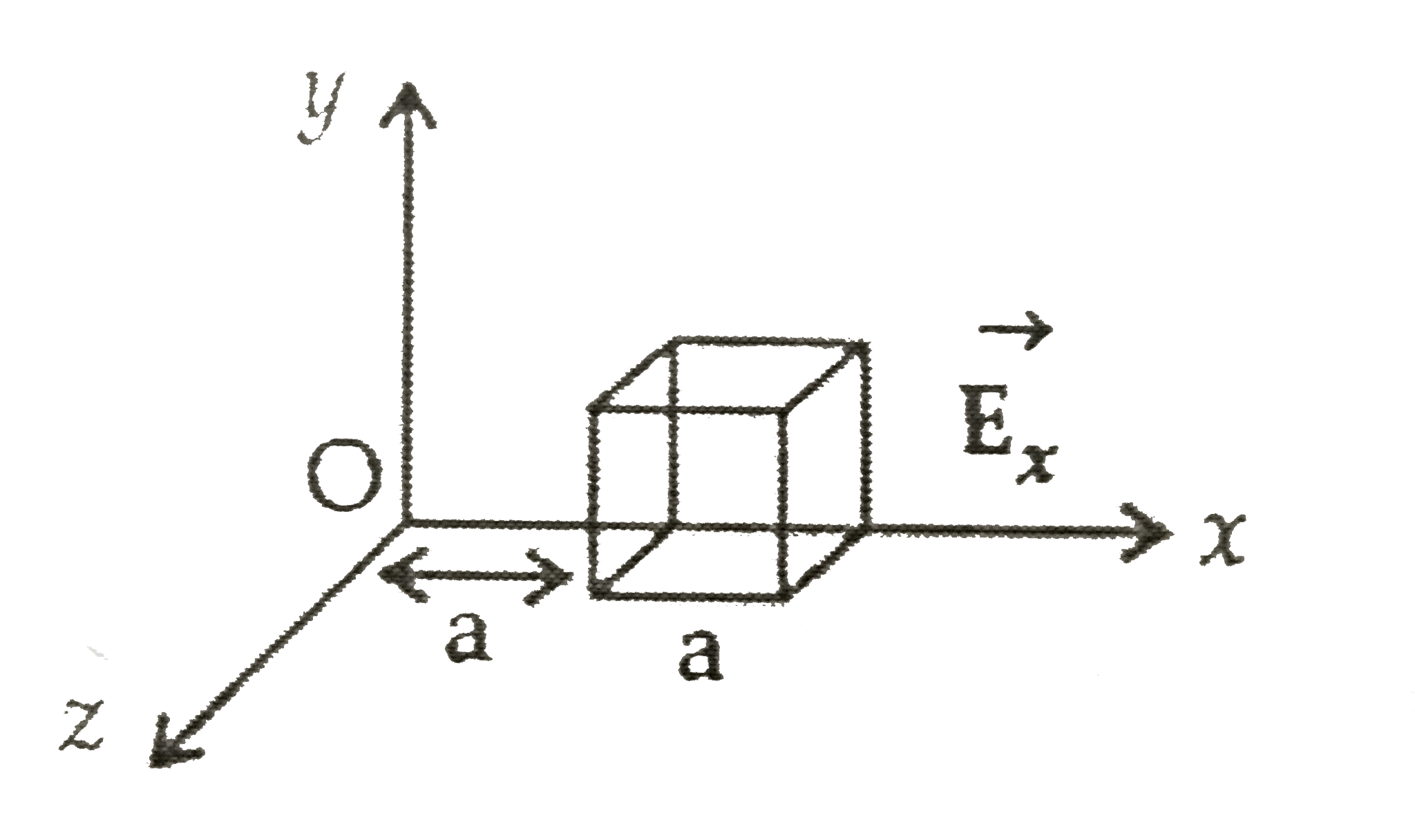
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.

Accroding the Gauss' law-
∮N,d→s=1eo{q}
∫→E−→ds1+∫→E−→ds2+∫−−→dS3=1∈o[λL]
∫Eds1Cos0+∫Eds2Cos90∘+∫Eds3Cos90∘=λL∈0
E∫ds1=λL∈0
E×2πrL=λL∈0
E=λ2π∈0r
→E=λ2π∈erˆr
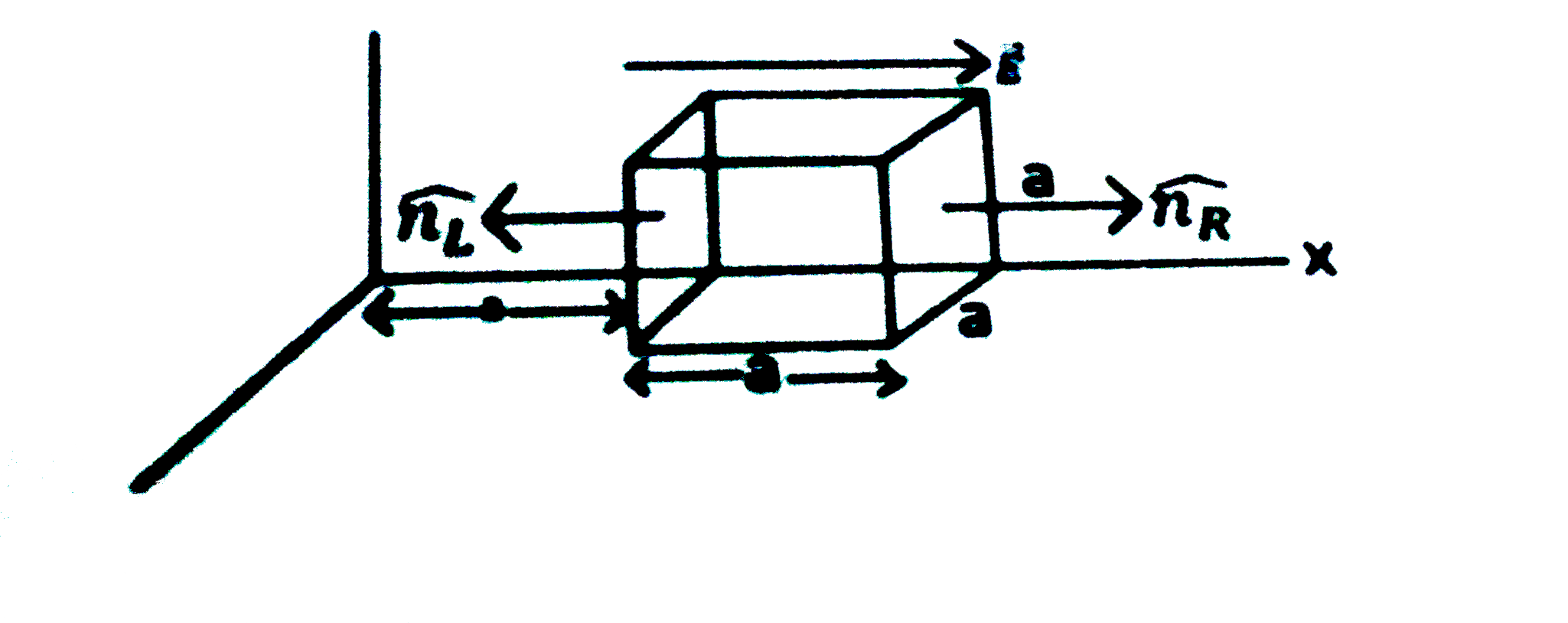
∴Ex=∝x=400x
Ey=Ez=0
Hence flux will exist onlt on left and right faces of cubt as Ex≠0
∴→EL⋅a2(n2)+→ER⋅a2ˆnR=1∈0{q∈}=ϕ
−EL⋅a2ˆ(n2)+a2ER=πNet
ϕNet=−(400a)a2+a2(400×2a)
≡400a3+800a3
=400a3
=400×(.1)3
ϕNet=0.4Nm2c−1
∴ϕNet=1∈0{q∈}
∴q∈=∈0ϕNet
8.85×10−12×0.4
=3.540×10−12c
Topper's Solved these Questions
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION C
8 Videos
- EXAM REVISION SERIESBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - EXAM REVISION SERIESEXERCISE - All Questions
41 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - B
7 Videos
Similar Questions
Using Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
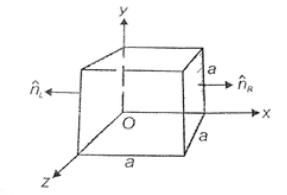
View SolutionThe electric field components in the figure below are Ex=800x2N/C,Ey=Ez=0.
Calculate
(1) The flux throught he cube and
(2) The charge withing the cube
Assume that a =0.1 m
View SolutionAnswer the following:
State Gauss' law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire.
View SolutionDefine electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .
View SolutionThe electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
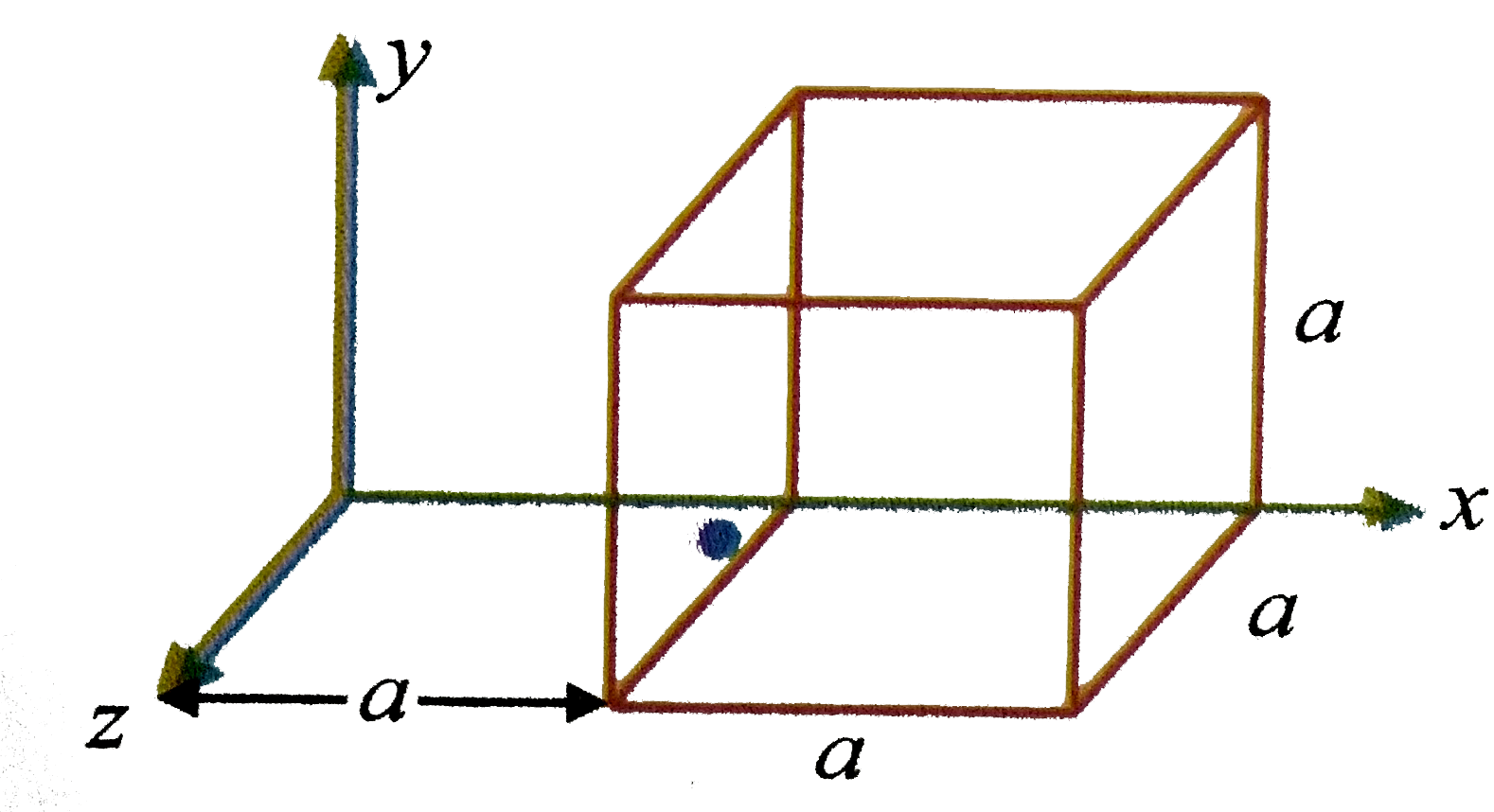
View Solution(a) Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
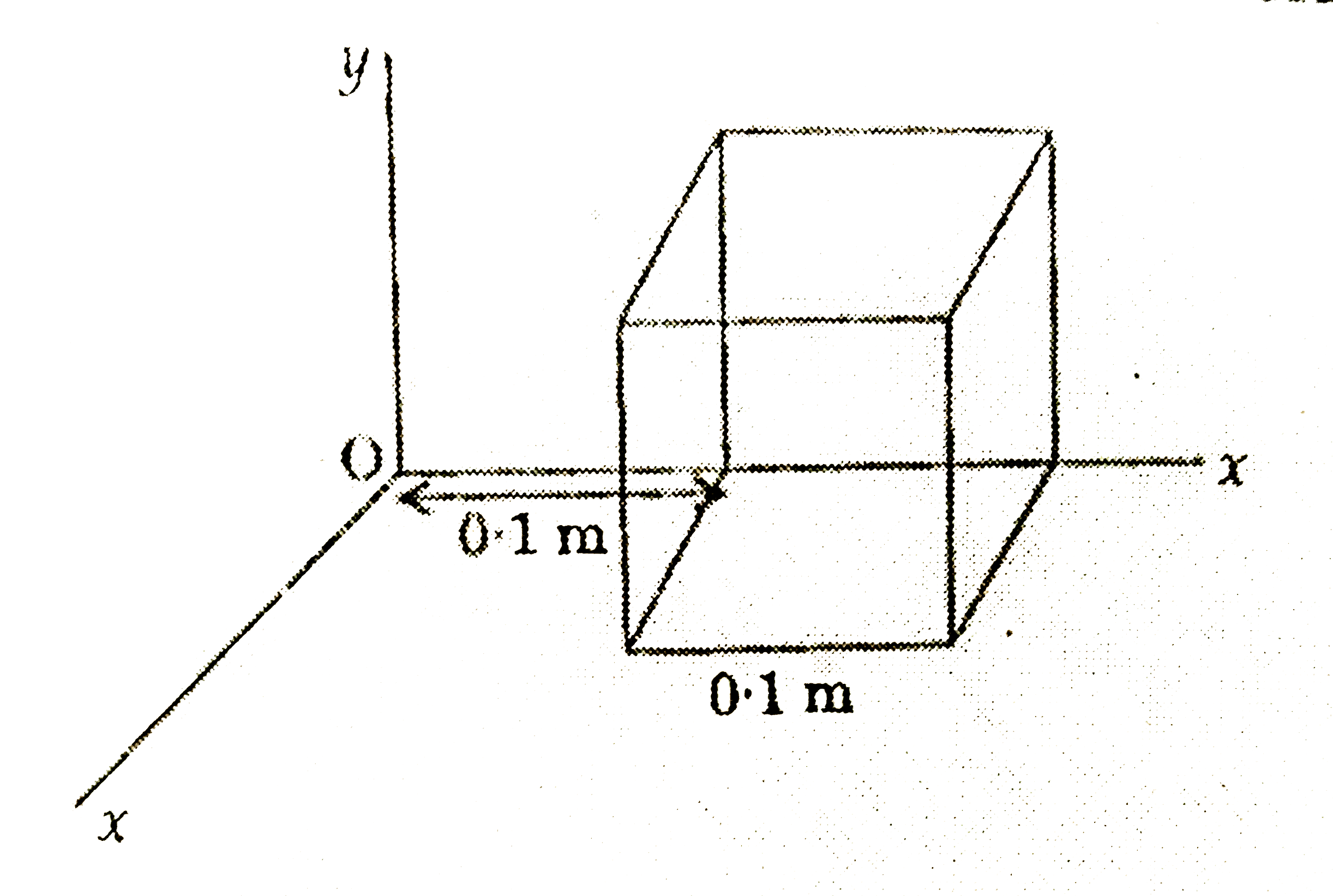
Ex=αx, where α=500N/C−m
Ey=0,Ez=0.
Calculate (i) the flux through the cube, and (ii) the charge inside the cube.
View Solution(a) Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
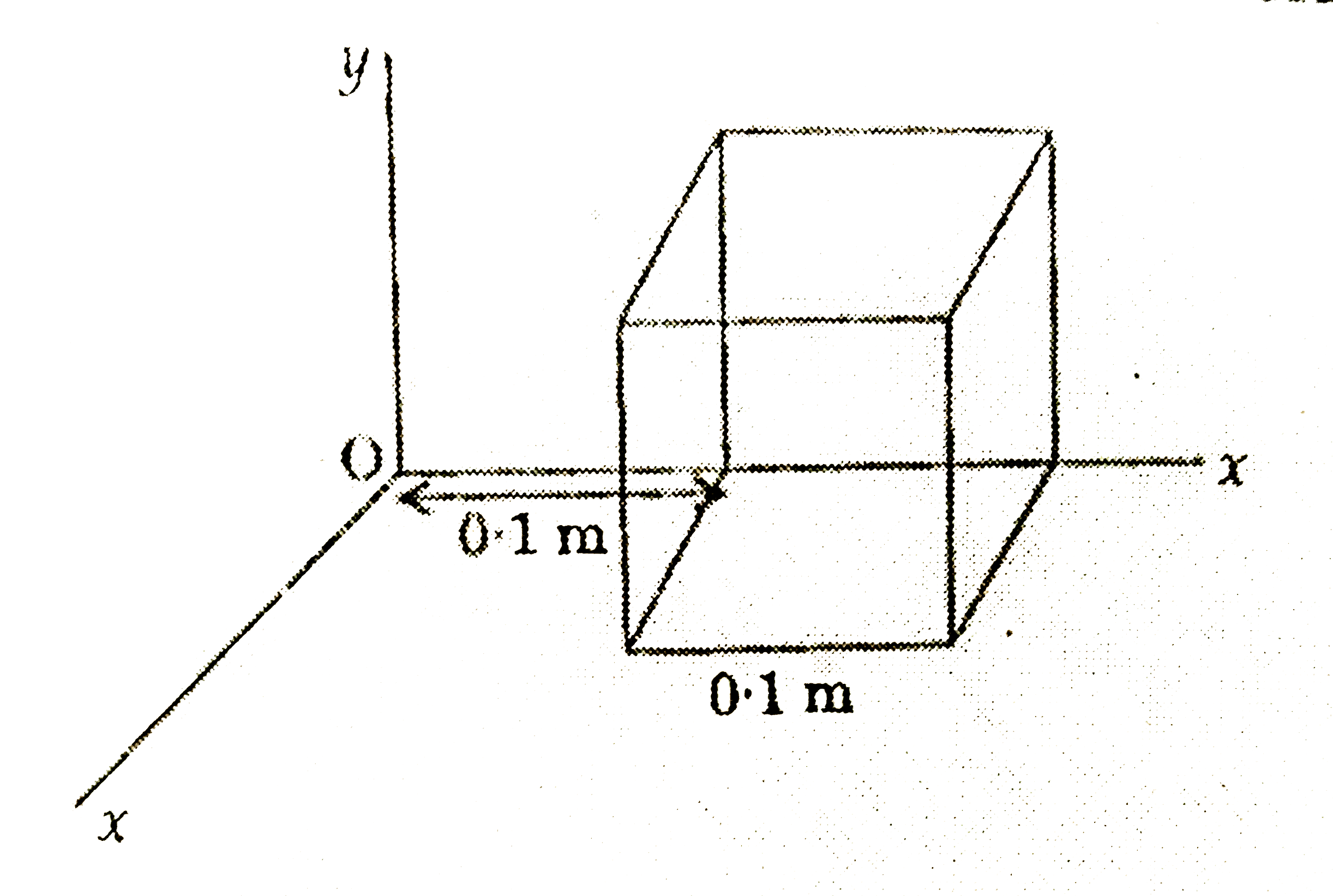
Ex=αx, where α=500N/C−m
Ey=0,Ez=0.
Calculate (i) the flux through the cube, and (ii) the charge inside the cube.
View SolutionState Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionUsing Gauss. theorem, obtain an expression for intensity of electric field .E. at a point which is at a distance r (r>R) from the centre Cof a thin spherical shell (of radius R) carrying charge.Q.
View SolutionThe maximum electric field at a point on the axis of a uniformly charged ring is E0. At how many points on the axis will the magnitude of the electric field be E0/2.
View Solution
