Answer the following:
State Gauss' law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire.
Step-by-Step Solution
Step 1: State Gauss's Law in Electrostatics
Gauss's Law states that the total electric flux (Φ_E) through a closed surface is equal to the charge (Q) enclosed by that surface divided by the permittivity of free space (ε₀). Mathematically, it can be expressed as:
ΦE=∮→E⋅d→A=Qϵ0
where:
- ΦE is the electric flux,
- →E is the electric field,
- d→A is the differential area vector,
- Q is the total charge enclosed,
- ϵ0 is the permittivity of free space.
---
Step 2: Consider the Configuration of the Problem
To derive the electric field due to an infinitely long straight uniformly charged wire, we consider a wire with a linear charge density (λ), which is the charge per unit length.
Let:
- λ = charge per unit length (C/m)
- r = distance from the wire to the point where we want to calculate the electric field
- L = length of the wire (considered to be infinitely long)
---
Step 3: Choose a Gaussian Surface
We select a cylindrical Gaussian surface of radius r and length L that is coaxial with the charged wire. This means the axis of the cylinder aligns with the wire.
---
Step 4: Determine the Electric Field Symmetry
Due to the symmetry of the problem, the electric field E at any point on the cylindrical surface will be the same in magnitude and directed radially outward from the wire. Thus, we can express the electric field as a function of r.
---
Step 5: Calculate the Electric Flux
The total electric flux through the cylindrical surface can be calculated using Gauss's Law:
ΦE=∮→E⋅d→A=E⋅A
Here, A is the curved surface area of the cylinder, which is given by:
A=2πrL
Thus, the electric flux becomes:
ΦE=E⋅(2πrL)
---
Step 6: Calculate the Charge Enclosed
The charge enclosed by the Gaussian surface is given by:
Q=λL
where λ is the linear charge density.
---
Step 7: Apply Gauss's Law
According to Gauss's Law:
∮→E⋅d→A=Qϵ0
Substituting the expressions for electric flux and charge, we have:
E⋅(2πrL)=λLϵ0
---
Step 8: Solve for the Electric Field E
We can simplify the equation by canceling L from both sides (assuming L≠0):
E⋅(2πr)=λϵ0
Now, solving for E:
E=λ2πϵ0r
---
Conclusion: Final Expression for the Electric Field
The electric field E due to an infinitely long straight uniformly charged wire is given by:
E=λ2πϵ0r
---
- ΦE is the electric flux,
- →E is the electric field,
- d→A is the differential area vector,
- Q is the total charge enclosed,
- ϵ0 is the permittivity of free space.
- λ = charge per unit length (C/m)
- r = distance from the wire to the point where we want to calculate the electric field
- L = length of the wire (considered to be infinitely long)
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]
Explore 11 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)
Explore 5 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SECTION-B
Explore 52 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
Using Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionState Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionAnswer the following:
(a) State Gauss' law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
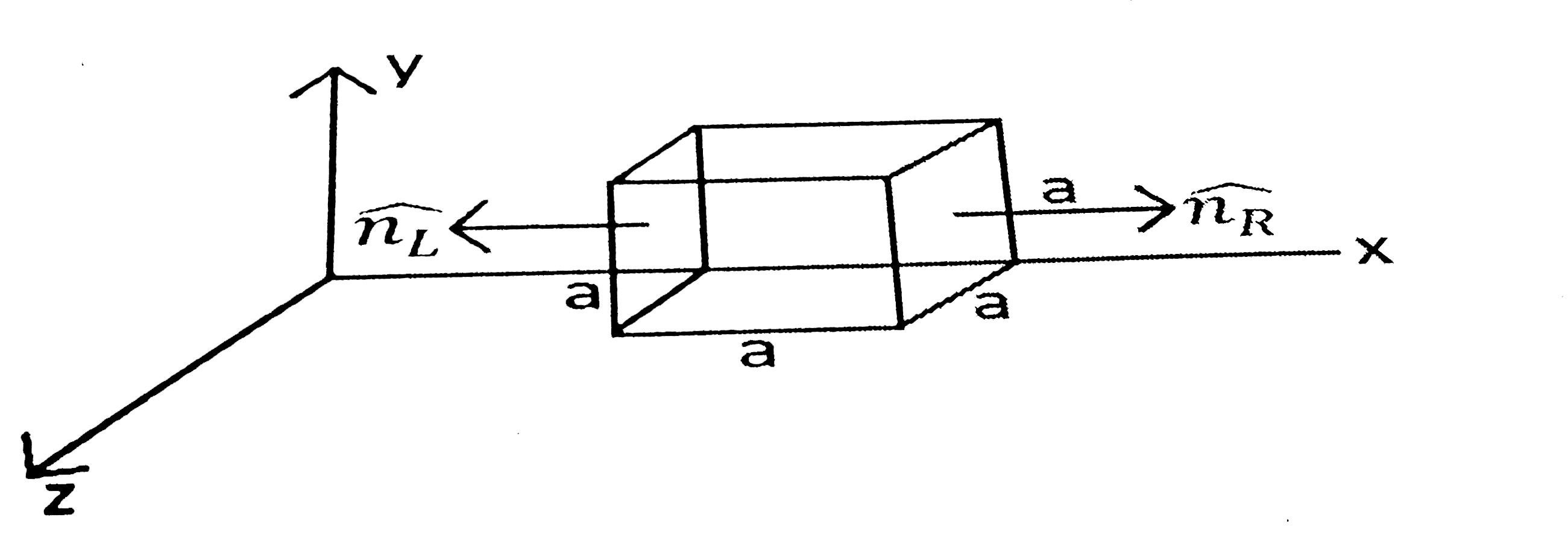
View SolutionAnswer the following:
(i) Use Gauss' law to find the electric field due to a uniformly charged infinite plane sheet. What is the direction of field for positive and negative charge densities?
(ii) Find the ratio of the potential differences that must be applied across the parallel and series combination of two capacitors C1 and C2 with their capacitance in the ratio 1:2 so that the energy stored in the two cases becomes the same.
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View Solution(a) Use Gauss's law to derive the expression for the electric filed (→E) due to straight uniformaly charges infinite line of charges density λC/m.
(b) Draw a graph to show the variation of E with perpendicular from the line of charge.
(c) Find the work done in brining a charge q from prependicular distance r1 to r2(r2>r1).
View Solution

