Question

Use Gauss's law to derive the expression for the electric field between two uniformly charged large parallel sheets with surface charge densities $\sigma$ and $-\sigma$ respectively.

Explanation

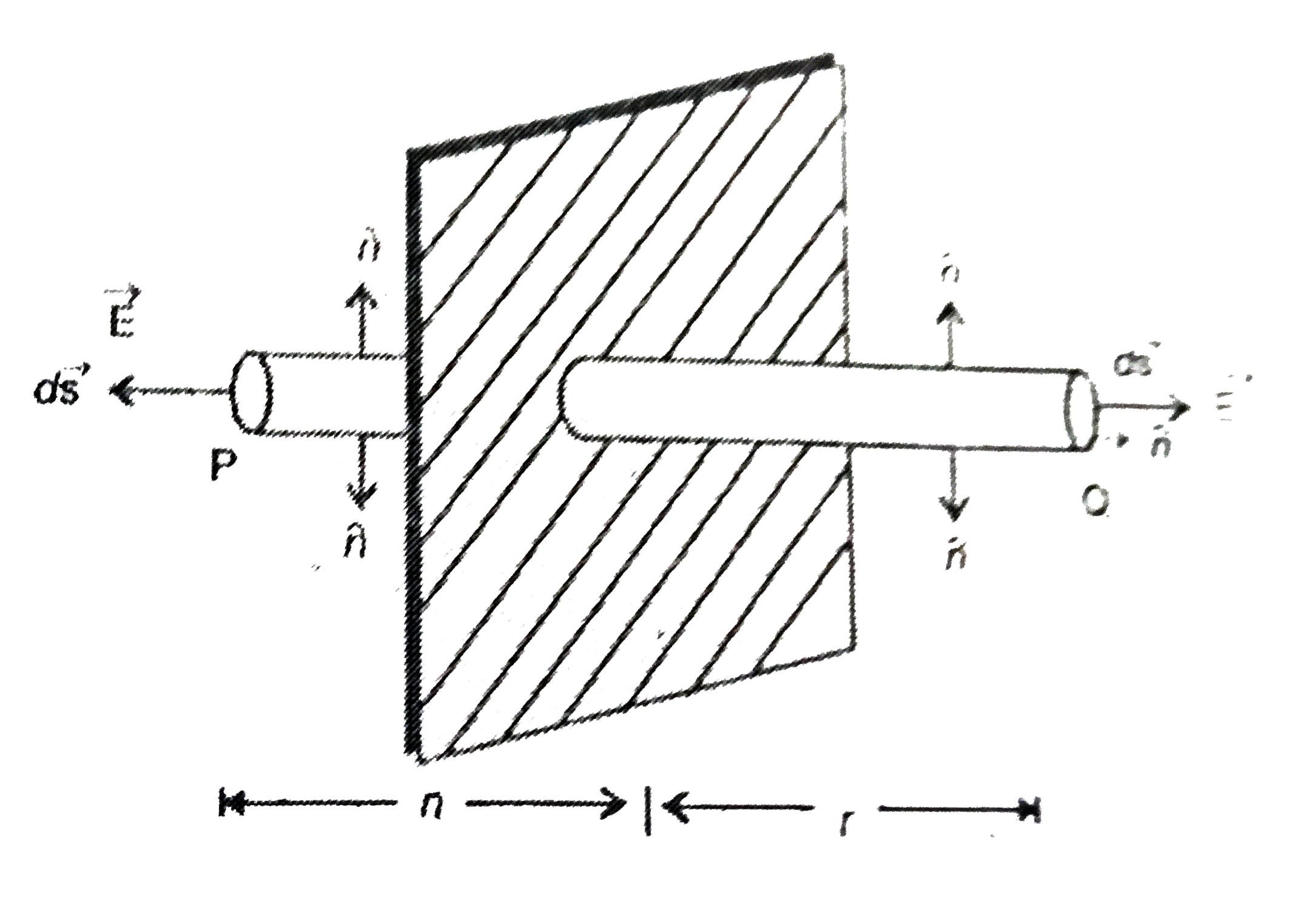
Electric field due to a uniformly charged infinite plane sheet : Suppose a thin non-conducting uniform surface charge density `sigma`.
Electric field intensity `vec(E)` on either side of the sheet must be perpendicular to the plane of sheet having same magnitude at all points equidistant from sheet.
Let P be any point at a distance r from the sheet. Let the small area element `vec(dS)=dS hat(n)`.
`vec(E)` and `hat(n)` are perpendicular on the surface of imagined cylinder, so electric flux is zero.
`vec(E)` and `hat(n)` are parallel on the two cylindrical edges P and Q which contributes electric flux.
`:.` Electric flux over the edges Pand Q of the cylinder is
`2 phi=q/epsi_(0) implies 2 oint vec(E) vec(dS). =q/epsi_(0)`

`implies 2 oint vec(E)vec(dS). = q/epsi_(0)`
`implies 2 oint E dS=q/epsi_(0)``implies 2 E pi r^(2)=q/epsi_(0) implies E=q/(2pi epsi_(0) r^(2))`
`:.` The charge density `sigma=q/S`
`implies q= pi r^(2) sigma`
`E=(pi r^(2) sigma)/(2 pi epsi_(0) r^(2))`
`E= sigma/(2 epsi_(0))`, vectorically `vec(E)= sigma/(2 epsi_(0)) hat(n)`
Where `hat(n)` is a unit vector normal to the plane and going away from it. where `sigma gt 0` E is directed away from both sides.
Now consider two infinite plane parallel sheets of charge A and B. Let `sigma_(1)=sigma` and `sigma_(2)=- sigma` be the uniform surface density of charge on A and B respectively.
The electric field between two plates is given by
`E=E_(1)-E_(2)`
`=sigma_(1)/(2 epsi_(0))-sigma_(2)/( 2 epsi_(0))=sigma/(2 epsi_(0))-((-sigma)/(2epsi_(0)))=(sigma+sigma)/(2epsi_(0))`
`:. E=(2 sigma)/(2 epsi_(0)) implies E= sigma/epsi_(0)`.