Two cells of equal e.m.f. E b ut of difference internal resistance r1 and r2 are connected in parallel and the combination is connected with an external resistance R to obtain maximum power in R. find the value of R

Let us consider the ball as the body A and the wedge as the body B. Before collision let velocity of ball is u^a after the impact, the ball bounces with velocity vA and the wedge advances in horizontal direction with velocity vB. These velocities and their t and n-components are immediately before and after the impact are shown in the following figures.

Component along t-axis The ball is free to move before and after the impact, therefore its t-component of momentum conserved. hence, t-component of velocities of the ball remains unchanged.
vAt=UAt=10cos37.=8m/s ...(i)
Momentum Conservation In the horizontal direction, there is no extrnal force on both the bodies. Therefore horizontal component of total momentum of both the bodies remain conserved. mAuA=mA(vAtcos37.−vAncos53.)+mBvB
0.25×10=0.25(8×45−3vAn5)+0.72vB
Coefficient of restitution Concept of coefficient of restitution e is applicable only for the n-component velocities.
vBn−vAn=e(uAn−UBn)→3vB5−vAn=0.8(6−0) ...(iii)
From equations (i), (ii) and (iii), we obtain vB=2.0m/s
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III
26 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
Two batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionTwo cells of emf E1 and E2 have internal resistance r1 and r2. Deduce an expression for equivalent emf of their parallel combination.
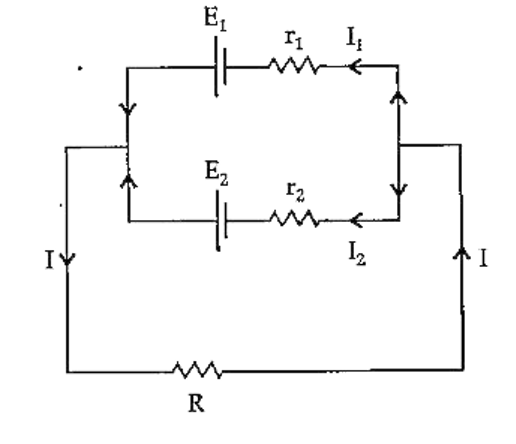
View SolutionTwo batteries of emf E1andE2(E2>E1) and internal resistances r1andr2 respectively are connected in parallel as shown in figure.

View SolutionTwo cells of same emf E, but different internal resistances r1andr2 are connected to an external
resistance R as shown in the figure given above. The voltmeter V reads zero. Obtain an expression for R in terms of r1andr2. Calculate the voltage across the cell of internal resistance r2. (Assume that the voltmeter V is of infinite resistance).
View SolutionFive cells each of emf E and internal resistance r are connecte in series. Due to oversight one cell is connected wrongly . The equivalent emf and internal resistance of the combination is
View Solution
Two batteries of E1 internal resistance r1 & emf E2 internal resistance r2 are connected in parallel and makes a battery system. An external resistance R is connected across this system as shown in the figure.
View SolutionConsider N=n1n2indentical cells, each of emf(ε) and internal resistance r. Suppose n1 cells are joined in series to forn a line and n_(2) such are connected in parallel. The combination drives a current in an external resistance R.(a) find the current in the external resistance, (b) Assuming that n1and n_(2) can be continuously varied, find the relation between n_(1) ,n_(2) R and r for which the current in R in maximum.
View SolutionTwo cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
View Solution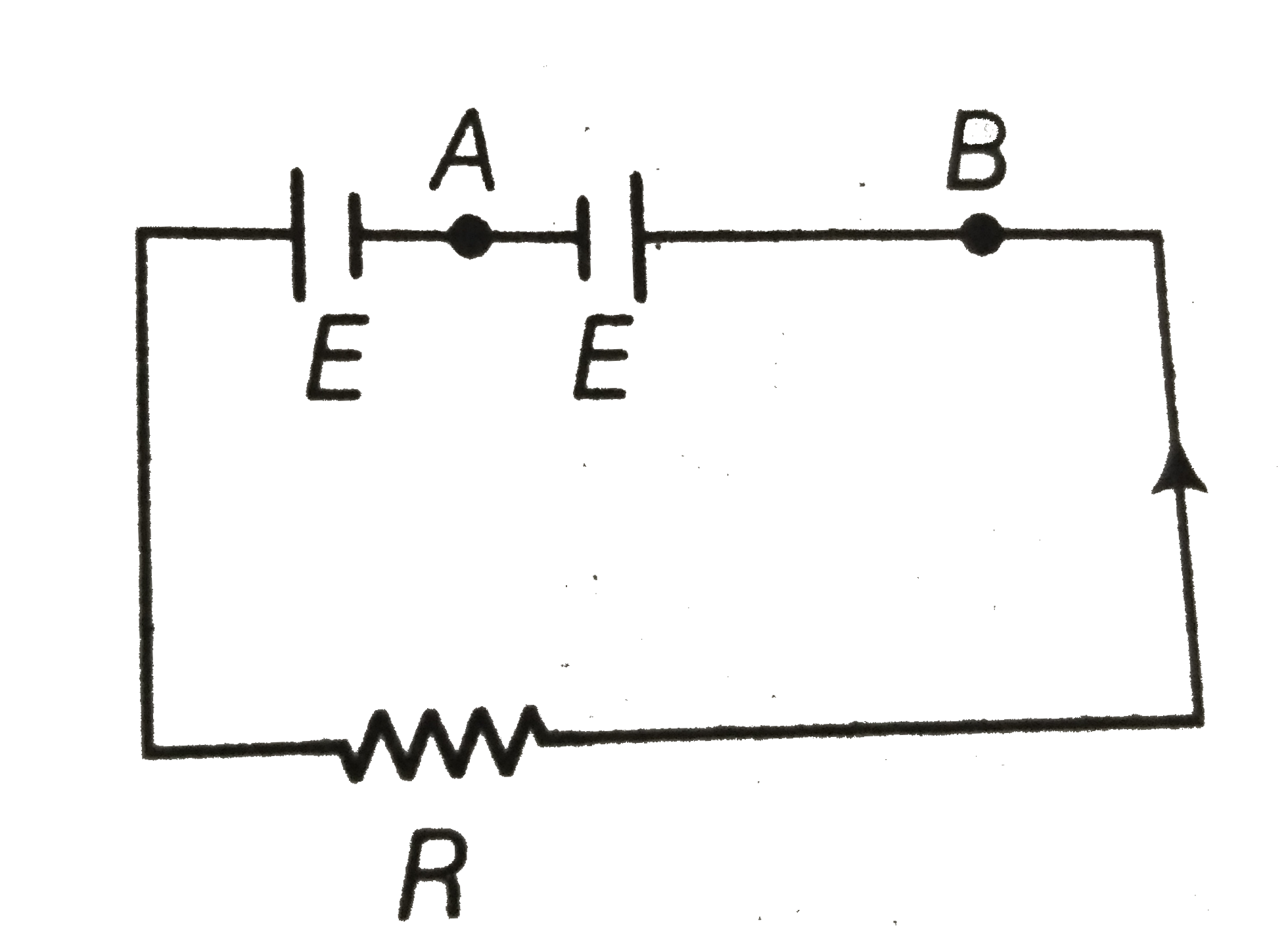
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?
View Solution
