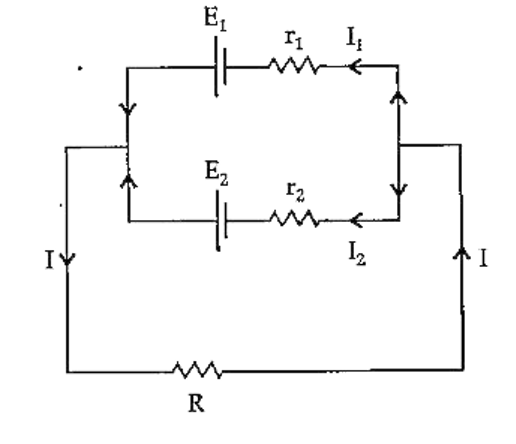
Two cells of same emf E, but different internal resistances $r_{1} and r_{2}$ are connected to an external
resistance R as shown in the figure given above. The voltmeter V reads zero. Obtain an expression for R in terms of $r_{1} and r_{2}$ . Calculate the voltage across the cell of internal resistance $r_{2}$ . (Assume that the voltmeter V is of infinite resistance).

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the circuit with two cells of the same emf $E$ but different internal resistances $r_{1}$ and $r_{2}$ connected to an external resistance $R$ . The voltmeter $V$ reads zero, which indicates that there is no potential difference across it.
1. Understanding the Circuit:
- We have two cells in series, each with an emf $E$ and internal resistances $r_{1}$ and $r_{2}$ .
- The total emf in the circuit is $2 E$ (since both cells contribute).
- The total internal resistance is $r_{1} + r_{2}$ .
2. Applying Kirchhoff's Loop Rule:
- According to Kirchhoff's loop rule, the sum of the potential differences around a closed loop is zero.
- The equation can be written as:
$2 E - I (R + r_{1} + r_{2}) = 0$
- Here, $I$ is the current flowing through the circuit.
3. Finding the Current $I$ :
- Rearranging the equation gives:
$I = \frac{2 E}{R + r_{1} + r_{2}}$
4. Voltage Across the Internal Resistance $r_{2}$ :
- The voltage drop across $r_{2}$ can be calculated using Ohm's law:
$V_{r_{2}} = I \cdot r_{2}$
- Substituting the expression for $I$ :
$V_{r_{2}} = (\frac{2 E}{R + r_{1} + r_{2}}) \cdot r_{2}$
5. Condition for Voltmeter Reading Zero:
- The voltmeter reads zero when the potential difference across it is zero, which means:
$E - I r_{1} = 0$
- Thus, we can write:
$E = I r_{1}$
- Substituting $I$ from the previous step:
$E = (\frac{2 E}{R + r_{1} + r_{2}}) r_{1}$
6. Solving for $R$ :
- Rearranging gives:
$E (R + r_{1} + r_{2}) = 2 E r_{1}$
- Dividing both sides by $E$ (assuming $E \neq 0$ ):
$R + r_{1} + r_{2} = 2 r_{1}$
- Therefore:
$R = 2 r_{1} - r_{1} - r_{2} = r_{1} - r_{2}$
Final Expressions:
- The expression for the external resistance $R$ in terms of $r_{1}$ and $r_{2}$ is:
$R = r_{1} - r_{2}$
- The voltage across the cell with internal resistance $r_{2}$ is:
$V_{r_{2}} = \frac{2 E r_{2}}{R + r_{1} + r_{2}}$

Updated on:7/8/2024

|

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

In a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
A $R = r$
B $R < r$
C $R > r$
D $R = 0$

Recommended Questions

Home
Ask Doubt
Profile