A voltmeter of resistance RV and an ammeter of resistance RA are connected in series across a battery of emf E and of negligible internal resistance . When a resistance R is connected in parallel to volmeter , reading of ammeter increases to three times while that of volmeter reduces to one - third. Calculate RAandRV in terms of R.
To solve the problem, we need to analyze the circuit conditions before and after the resistance R is connected in parallel with the voltmeter. Let's break down the solution step by step.
Step 1: Define the initial conditions
Initially, we have a voltmeter with resistance RV and an ammeter with resistance RA connected in series across a battery of EMF E. The total resistance in the circuit is:
Rtotal=RA+RV
The current I1 flowing through the circuit can be expressed using Ohm's law:
I1=ERA+RV
Step 2: Calculate the voltmeter reading
The voltage across the voltmeter V1 can be calculated as:
V1=I1⋅RV=E⋅RVRA+RV
Step 3: Define the conditions after connecting resistance R in parallel
When resistance R is connected in parallel with the voltmeter, the equivalent resistance Req of the voltmeter and the resistance R is given by:
1Req=1RV+1R⟹Req=R⋅RVR+RV
Now the total resistance in the circuit becomes:
R′total=RA+Req=RA+R⋅RVR+RV
The new current I2 flowing through the circuit is:
I2=ERA+R⋅RVR+RV
Step 4: Relate the currents and voltmeter readings
According to the problem, the new current I2 is three times the initial current I1:
I2=3I1
Substituting the expressions for I1 and I2:
ERA+R⋅RVR+RV=3⋅ERA+RV
Since E is common, we can cancel it out:
1RA+R⋅RVR+RV=3RA+RV
Cross-multiplying gives:
RA+RV=3(RA+R⋅RVR+RV)
Step 5: Simplify the equation
Expanding and simplifying:
RA+RV=3RA+3R⋅RVR+RV
Rearranging terms:
RV−3RA=3R⋅RVR+RV
Cross-multiplying:
(RV−3RA)(R+RV)=3R⋅RV
Step 6: Analyze the voltmeter reading
The new voltmeter reading V2 is one-third of the initial reading:
V2=V13
Substituting for V2:
E⋅ReqRA+Req=13⋅E⋅RVRA+RV
Again canceling E and rearranging gives:
3Req=RV⋅RA+RV⋅ReqRA+RV
Step 7: Solve the equations
We now have two equations to work with. By substituting Req into the equations and solving for RA and RV in terms of R, we can derive the values.
After solving the equations, we find:
RV=8RandRA=8R3
Final Answer
Thus, the values of the resistances are:
RV=8RandRA=8R3
Initially, we have a voltmeter with resistance RV and an ammeter with resistance RA connected in series across a battery of EMF E. The total resistance in the circuit is:
Rtotal=RA+RV
The current I1 flowing through the circuit can be expressed using Ohm's law:
I1=ERA+RV
The voltage across the voltmeter V1 can be calculated as:
V1=I1⋅RV=E⋅RVRA+RV
When resistance R is connected in parallel with the voltmeter, the equivalent resistance Req of the voltmeter and the resistance R is given by:
1Req=1RV+1R⟹Req=R⋅RVR+RV
Now the total resistance in the circuit becomes:
R′total=RA+Req=RA+R⋅RVR+RV
The new current I2 flowing through the circuit is:
I2=ERA+R⋅RVR+RV
According to the problem, the new current I2 is three times the initial current I1:
I2=3I1
Substituting the expressions for I1 and I2:
ERA+R⋅RVR+RV=3⋅ERA+RV
Since E is common, we can cancel it out:
1RA+R⋅RVR+RV=3RA+RV
Cross-multiplying gives:
RA+RV=3(RA+R⋅RVR+RV)
Expanding and simplifying:
RA+RV=3RA+3R⋅RVR+RV
Rearranging terms:
RV−3RA=3R⋅RVR+RV
Cross-multiplying:
(RV−3RA)(R+RV)=3R⋅RV
The new voltmeter reading V2 is one-third of the initial reading:
V2=V13
Substituting for V2:
E⋅ReqRA+Req=13⋅E⋅RVRA+RV
Again canceling E and rearranging gives:
3Req=RV⋅RA+RV⋅ReqRA+RV
We now have two equations to work with. By substituting Req into the equations and solving for RA and RV in terms of R, we can derive the values.
RV=8RandRA=8R3
Thus, the values of the resistances are:
RV=8RandRA=8R3
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -4 (Level -I)
37 Videos
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -4 (Level -II)
25 Videos
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -3 (Level -II) SECTION E- Electrical Power & Energy
3 Videos
- CONSTRAINED MOTION BOOK - MOTIONCHAPTER - CONSTRAINED MOTION EXERCISE - EXAMPLES
12 Videos
- ELASTICITYBOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - EXERCISE -3
60 Videos
Similar Questions
A voltmeter of resistance R1 and an ammeter of resistance R2 are connected in series across a battery oif negligible internal resistance. When as resistance R is connected in parallel to voltmeter reading of ammeter increases three times white that of voltmeter reduces to one third. Find R1 and R2 in terms of R.
View SolutionAn ammeter of zero resistance and a volt meter are connected in series to a battery of emf 6.0 volt and certain internal resistance. When a resistance R is connected in parallel with the voltmeter the readings of the voltmeter becomes half of its initial reading and the reading of the ammeter becomes 2 times to its initial reading (before R is connected). Find the voltmeter reading in volt after the connection of the resistance.
View Solution
Knowledge Check
An ammeter and a voltmeter of resistance R are connected in series to an electric cell of negligible internal resistance . Their readings are A and V respectively. If another resistance R is connected in parallel with the voltmeter , then
ABoth A and V increasesBBoth A and V decreasesCA decreases but V increasesDA increases but V decreases.An ammeter and a voltmeter of resistance R are connected in series to an electric cell of negligible internal resistance . Their readings are A and V respectively. If another resistance R is connected in parallel with the voltmeter , then
ABoth A and V will increaseBBoth A and V will decreaseCA will decrease and V will increaseDA will increase and V will decreaseAn ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
ABoth A and V will increaseBBoth A and V will decreaseCA will decrease and V will increaseDA will decrease and V will decrease
A voltmeter of resistance RV and an ammeter of resistance RA are connected as shown in an attempt to measure the resistance R. The measured value of the resistance is RM=VI0 where V is reading of voltmeter and I0 is reading of the ammeter. find the true value of the resistance in terms of RM,RVandRA.
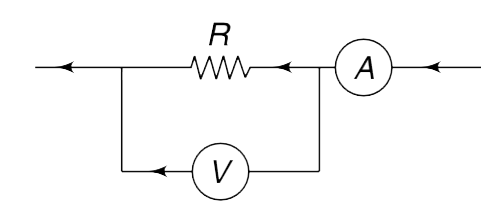
View SolutionAn ammeter and a voltmeter are connected in series to a battery with an emf ξ=6.0V. When a certain resistance is connected in parallel with the voltmeter, the readings of the latter decreases η=2.0 times, whereas the readings of the ammeter increase the same number of times, Find the voltmeter readings after the connection of the resistance.
View SolutionAn ammeter, voltmeter and a resistor are connected in series to a cell and the readings are noted as I and V. If another resistor R is connected in parallel with a voltmeter, then
View SolutionAn ammeter and a voltmeter of resistance R are connected in series to an electric cell of negligible internal resistance . Their readings are A and V respectively. If another resistance R is connected in parallel with the voltmeter , then
View SolutionIn the circuit shows in Fig. 6.42, resistors X and Y, each with resistance R, are connected to a 6V battery of negligible internal resistance. A voltmetre, also of resistance R, is connected across Y.
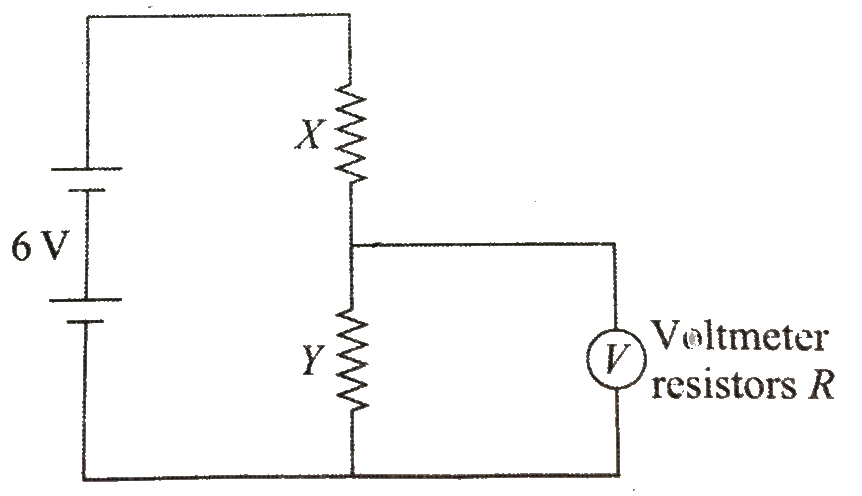
What is the reading of the voltmeter?
View Solution
