By a cell a current of 0.9 A flows through 2 ohm resistor and 0.3A through 7 ohm resistor. The internal resistance of the cell is
The correct Answer is:(i) at O, (ii) diagonally from O to 3 (iii) along OY', (iv) at O (v) diagonally from O to 4 (vi) at O
To find the internal resistance of the cell, we can follow these steps:
Step 1: Understand the Circuit
We have a cell with an internal resistance r, connected to two resistors: R1=2Ω and R2=7Ω. The current flowing through R1 is I1=0.9A and through R2 is I2=0.3A.
Step 2: Apply Ohm's Law
According to Ohm's law, the voltage across a resistor is given by:
V=I⋅R
For the first resistor:
V1=I1⋅R1=0.9⋅2=1.8V
For the second resistor:
V2=I2⋅R2=0.3⋅7=2.1V
Step 3: Write the Voltage Equation
The total voltage V provided by the cell can be expressed in terms of the internal resistance and the resistances:
V=I1⋅R1+I1⋅r(for the first case)
V=I2⋅R2+I2⋅r(for the second case)
Step 4: Set Up the Equations
From the first case:
V=0.9⋅2+0.9⋅r⇒V=1.8+0.9r(Equation 1)
From the second case:
V=0.3⋅7+0.3⋅r⇒V=2.1+0.3r(Equation 2)
Step 5: Equate the Two Voltage Expressions
Since both expressions equal V:
1.8+0.9r=2.1+0.3r
Step 6: Solve for r
Rearranging the equation gives:
0.9r−0.3r=2.1−1.8
0.6r=0.3
r=0.30.6=0.5Ω
Conclusion
The internal resistance of the cell is 0.5Ω.
---
We have a cell with an internal resistance r, connected to two resistors: R1=2Ω and R2=7Ω. The current flowing through R1 is I1=0.9A and through R2 is I2=0.3A.
According to Ohm's law, the voltage across a resistor is given by:
V=I⋅R
For the first resistor:
V1=I1⋅R1=0.9⋅2=1.8V
For the second resistor:
V2=I2⋅R2=0.3⋅7=2.1V
The total voltage V provided by the cell can be expressed in terms of the internal resistance and the resistances:
V=I1⋅R1+I1⋅r(for the first case)
V=I2⋅R2+I2⋅r(for the second case)
From the first case:
V=0.9⋅2+0.9⋅r⇒V=1.8+0.9r(Equation 1)
From the second case:
V=0.3⋅7+0.3⋅r⇒V=2.1+0.3r(Equation 2)
Since both expressions equal V:
1.8+0.9r=2.1+0.3r
Rearranging the equation gives:
0.9r−0.3r=2.1−1.8
0.6r=0.3
r=0.30.6=0.5Ω
The internal resistance of the cell is 0.5Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EXERCISE-IV B
Explore 14 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EXERCISE-V A
Explore 20 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EXERCISE-III
Explore 26 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE (J-A)
Explore 6 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
Similar Questions
The circuit diagram in Fig. shows three resistors 2Ω,4Ωand RΩ connected to a battery of e.m.f. 2 V and internal resistance 3 Ω. If current of 0.25 A flows through the circuit, find :
the p.d. across the internal resistance of the cell,
View SolutionA cell supplies a current i1 trhough a resistnace R1 and a current i2 through a resistance R2. The internal resistance of this cell is
View Solution
Knowledge Check
A current of 3A flows through the 2Ω resistor as shown in the circuit. The power dissipated in the 5Ω resistor is
 A5 watt.B4 watt.C2 watt.D1 watt
A5 watt.B4 watt.C2 watt.D1 wattCalculate the steady state current in the 2- ohm resistor shown in the circuit in the figure. The intermal resistance of the battery is negligible and the capacitance of the condenser C is 0.2 microfarad.
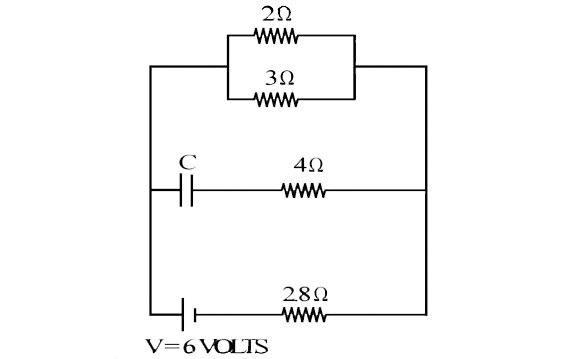 A0.6AB0.9AC1.2AD0.1A
A0.6AB0.9AC1.2AD0.1A
A current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View SolutionWhen two identical cells are connected either in series or in parallel across a 4 ohm resistor, they send the same current through it. The internal resistance of the cell in ohm is
View SolutionA 50V battery is connected across a 10 ohm resistor. The current is 4.5A is flowing through the resistor then the internal resistance of the battery is
View SolutionThe terminal voltage is E2 when a c urrent of 2A is flowing through 2Ω resistance, then the internal resistance of cell is:-
View SolutionDefine the emf (E) of a cell and the potential difference (V) across a resistor (R) in terms of the work done in moving a unit charge. State the relation between these two works and the work it charge through a cell connected across the resistor. Take the internal resistance of the cell as r. Hence, obtain expression for the current i in the circuit.
View Solution