Two cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
To solve the problem of finding the equivalent resistance and emf of two cells connected in parallel, we can follow these steps:
Step 1: Understanding the Circuit
We have two cells with emfs ϵ1 and ϵ2 and internal resistances r1 and r2 respectively connected in parallel. The total current I flowing from the combination can be expressed as the sum of the currents through each cell.
Step 2: Applying Kirchhoff's Voltage Law
For cell 1:
V=ϵ1−I1r1
For cell 2:
V=ϵ2−I2r2
Where I1 and I2 are the currents through cells 1 and 2 respectively, and V is the potential difference across the terminals of the parallel combination.
Step 3: Expressing Currents in Terms of Voltage
From the equations above, we can express the currents I1 and I2 as:
I1=ϵ1−Vr1
I2=ϵ2−Vr2
Step 4: Total Current in the Circuit
The total current I flowing from the combination is given by:
I=I1+I2
Substituting the expressions for I1 and I2:
I=ϵ1−Vr1+ϵ2−Vr2
Step 5: Rearranging the Equation
Rearranging the equation gives:
I=(ϵ1r1+ϵ2r2)−V(1r1+1r2)
Step 6: Identifying the Equivalent Voltage and Resistance
This equation can be compared to the standard form I=Eeq−VReq, where:
- The equivalent emf Eeq is given by:
Eeq=ϵ1r2+ϵ2r1r1+r2
- The equivalent resistance Req is given by:
Req=r1r2r1+r2
Final Expressions
Thus, the final expressions for the equivalent emf and resistance of the combination are:
1. Equivalent emf:
Eeq=ϵ1r2+ϵ2r1r1+r2
2. Equivalent resistance:
Req=r1r2r1+r2
We have two cells with emfs ϵ1 and ϵ2 and internal resistances r1 and r2 respectively connected in parallel. The total current I flowing from the combination can be expressed as the sum of the currents through each cell.
For cell 1:
V=ϵ1−I1r1
For cell 2:
V=ϵ2−I2r2
Where I1 and I2 are the currents through cells 1 and 2 respectively, and V is the potential difference across the terminals of the parallel combination.
From the equations above, we can express the currents I1 and I2 as:
I1=ϵ1−Vr1
I2=ϵ2−Vr2
The total current I flowing from the combination is given by:
I=I1+I2
Substituting the expressions for I1 and I2:
I=ϵ1−Vr1+ϵ2−Vr2
Rearranging the equation gives:
I=(ϵ1r1+ϵ2r2)−V(1r1+1r2)
This equation can be compared to the standard form I=Eeq−VReq, where:
- The equivalent emf Eeq is given by:
Eeq=ϵ1r2+ϵ2r1r1+r2
- The equivalent resistance Req is given by:
Req=r1r2r1+r2
Thus, the final expressions for the equivalent emf and resistance of the combination are:
1. Equivalent emf:
Eeq=ϵ1r2+ϵ2r1r1+r2
2. Equivalent resistance:
Req=r1r2r1+r2
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - D
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - E
5 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET -III, OUTSIDE DELHI]
3 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
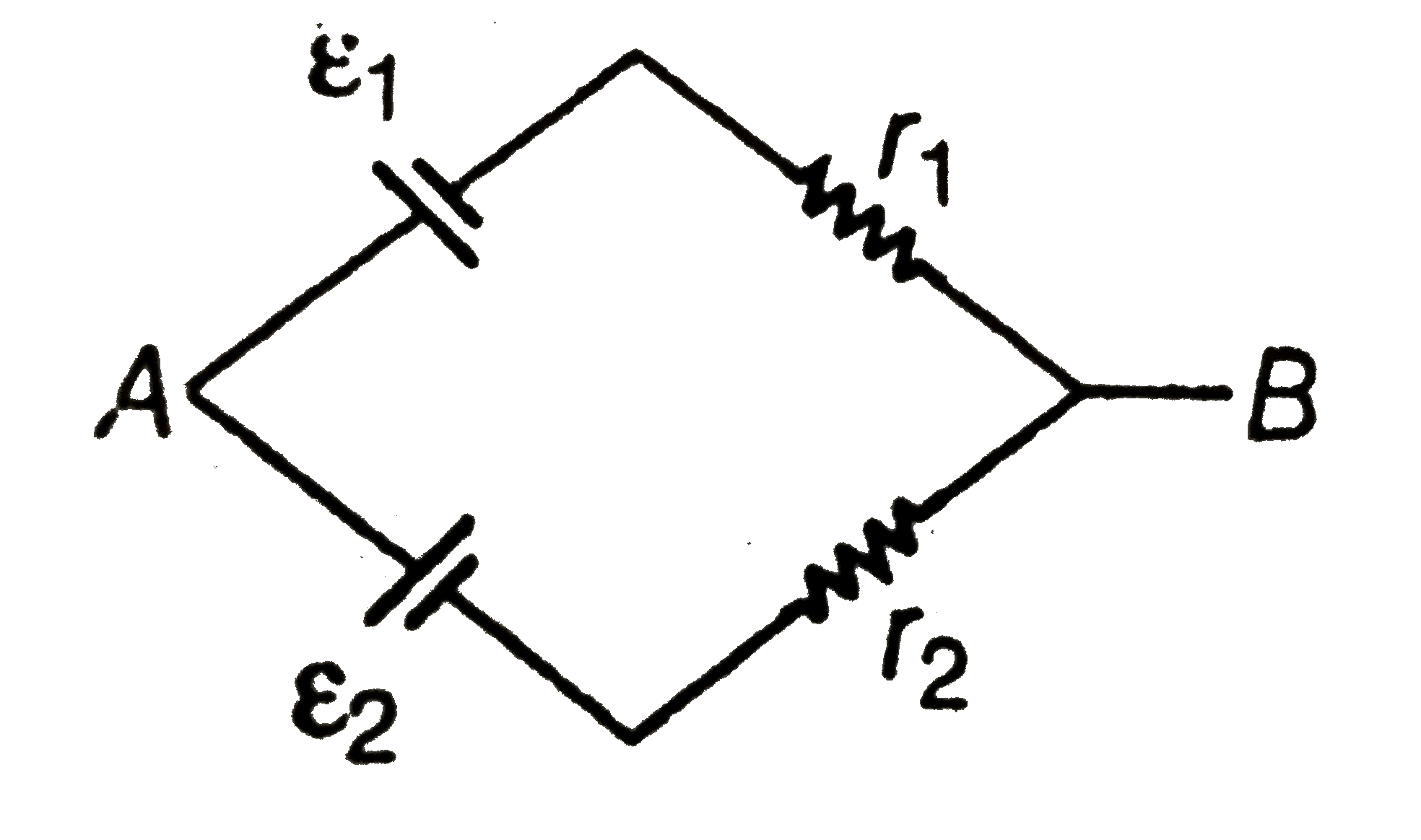
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.
View SolutionTwo batteries of emf E1andE2(E2>E1) and internal resistances r1andr2 respectively are connected in parallel as shown in figure.

View SolutionTwo batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.

View SolutionTwo batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.

View SolutionTwo batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.

View SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View SolutionTwo cells of emf E1 and E2 have internal resistance r1 and r2. Deduce an expression for equivalent emf of their parallel combination.
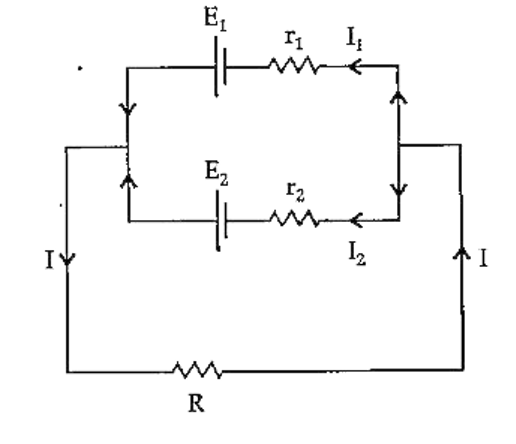
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
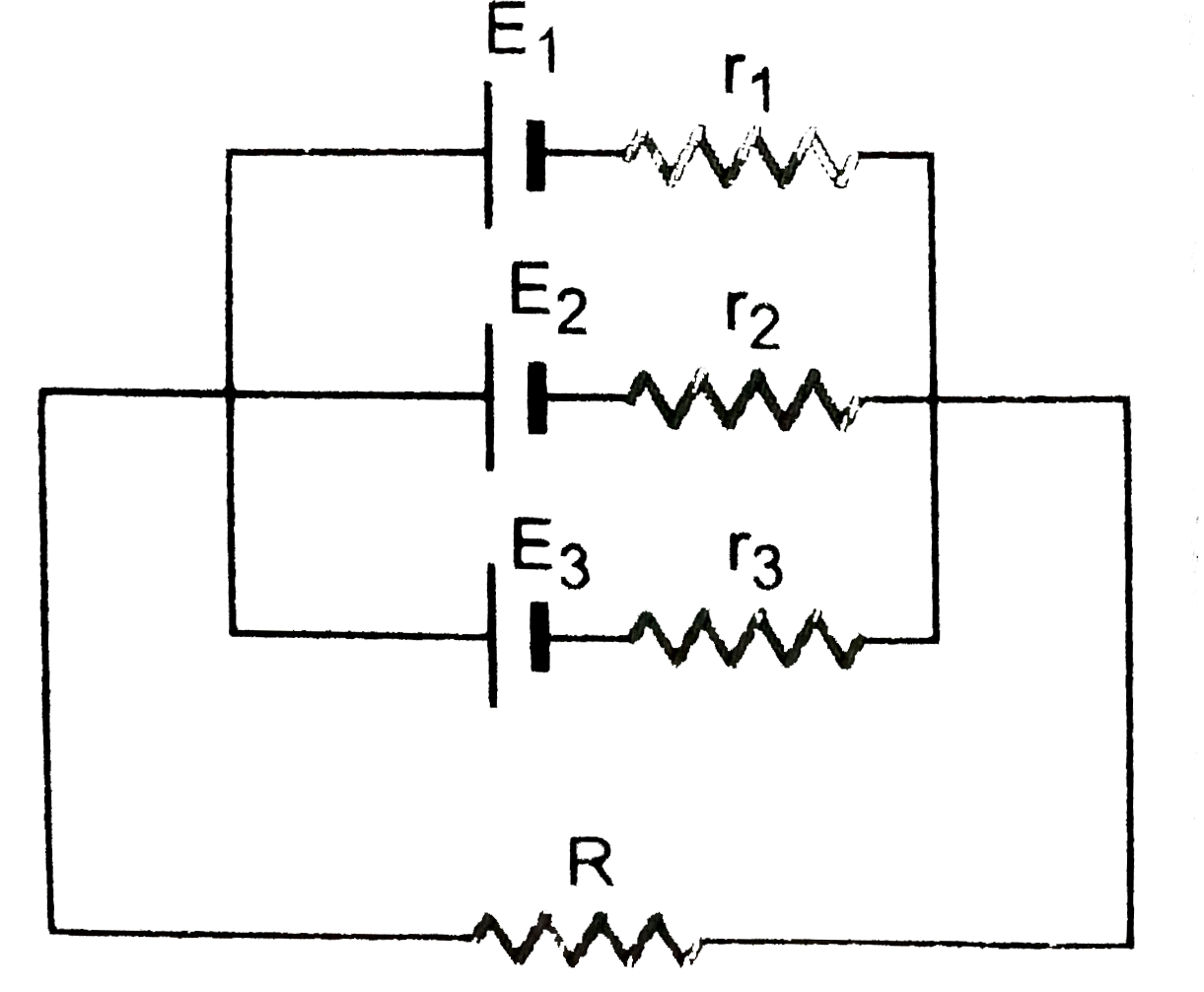
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
View SolutionShow by a diagram how two resistors R1andR2 are joined in parallel. Obtain an expression for the total resistance of the combination.
View Solution
