Two batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
(a) Let us consider the ball as the body A and the wall as the body B. Since the wall has infinte,y large inertia (mass) as compared to the ball, the state of motion of the wall, emains unaltered during the impact i.e. the wall remain stationary.
Now we show velocities of the ball and its t and n-components immediately before and after the impact. For the purpose we have assumed velocity of the ball after the impact v.

Component along t-axis Components of momentum along t-axis of the ball is conserved. Hence, t-component of velocities of each of the bodies remains unchanged. vt=ut=usinθ ...(i)
Component along -axis Concept of coefficient of restitution e is applicable only for the n-component velocities.
vBn−vAn=e(uAn−uBn)→−vn=eUn ,
From equations (i) and (ii), the t and n-components of velocity of the ball after the impact are
vt=usinθ and vn=eusinθ
(b) If the impact is perfectly elastic, we have vt=usinθ,vn=usinθ and θ=θ The ball will rebound with the same speed making the same angle with the vertical at which it has collided. In other words, a perfectly elastic collsion of a ball with a wall follows the same laws as light follows in reflection at a plane mirror.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III
26 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
Two batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
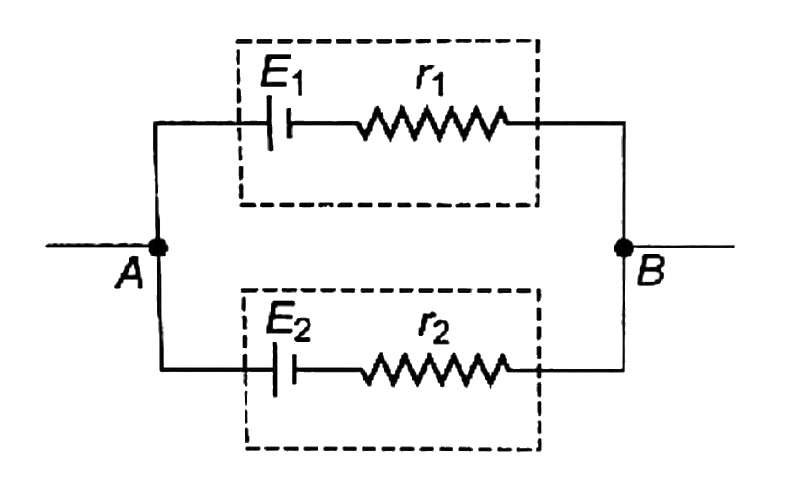
View SolutionTwo batteries of emf E1andE2(E2>E1) and internal resistances r1andr2 respectively are connected in parallel as shown in figure.

View Solution
Knowledge Check
Two batteries of emf e1ande2 having internal resistance r1andr2 respectively are connected in series to an external resistance R. Both the batteries are getting discharged. The above described combination of these two batteries has to produce a weaker current than when any one of the batteries is connected to the same resistor. For this requirement to be fulfilled
Aε2ε1must not lie betweenr2r1+Randr1r2+RBε2ε1must not lie betweenr2r1+Randr2+Rr1Cε2ε1must lie betweenr2r1+Randr1r2+RDε2ε1must not lie betweenr2r1+Randr2+Rr1
The two batteries of emf E1 and E2 having internal resistances r1 and r2 respectively are connected in series to an external resistor R. Both the batteries are gatting discharged. The above described combination of these two batteries has to produce a weaker current then when any one of the battery is connected to same resistor. For this requirement to be fulfilled.
View SolutionTwo cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
View Solution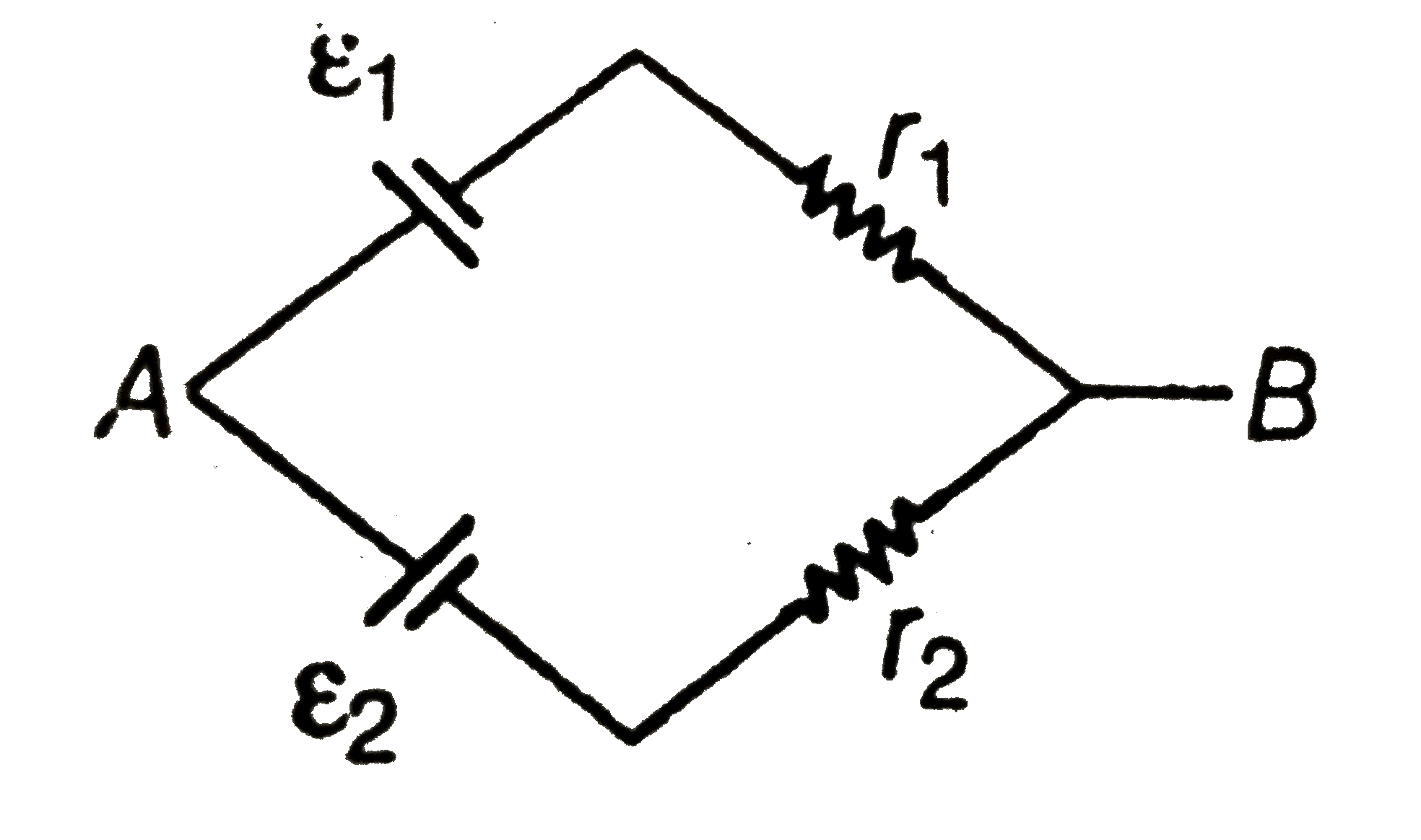
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.
View SolutionFind the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure

View SolutionTwo cells of emf E1 and E2 have internal resistance r1 and r2. Deduce an expression for equivalent emf of their parallel combination.
View SolutionTwo cells of equal e.m.f. E b ut of difference internal resistance r1 and r2 are connected in parallel and the combination is connected with an external resistance R to obtain maximum power in R. find the value of R

View Solution
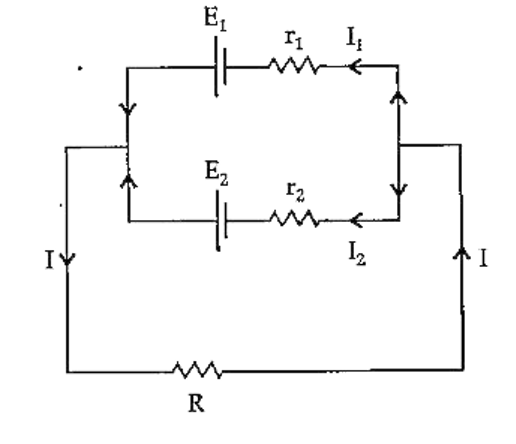
Two batteries of E1 internal resistance r1 & emf E2 internal resistance r2 are connected in parallel and makes a battery system. An external resistance R is connected across this system as shown in the figure.
View Solution
