Question

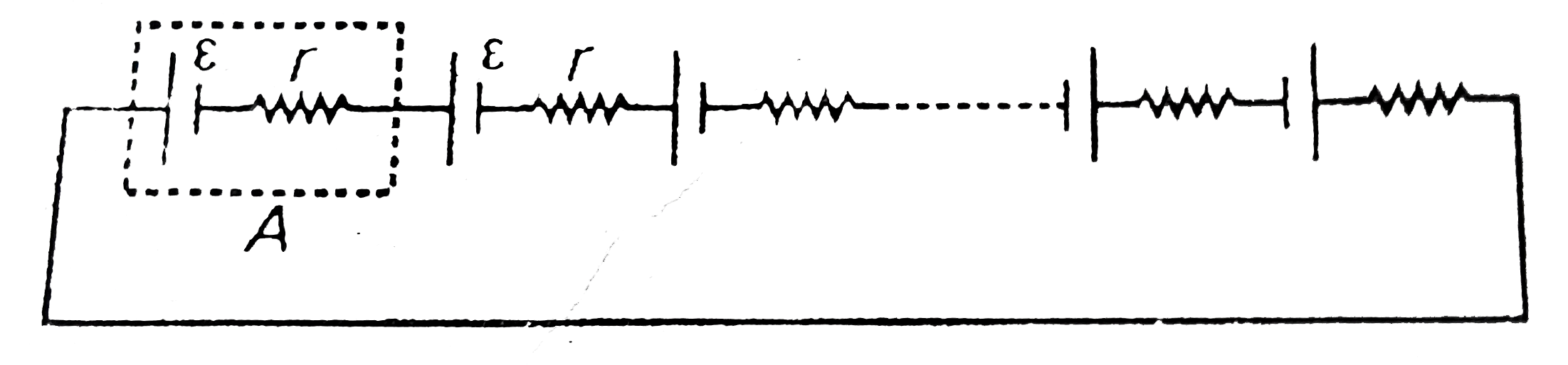
Consider $N=n_1{n}_2$indentical cells, each of emf$\left(\epsilon \right)$ and internal resistance r. Suppose $n_1$ cells are joined in series to forn a line and n_(2) such are connected in parallel. The combination drives a current in an external resistance R.(a) find the current in the external resistance, (b) Assuming that $n_1$and n_(2) can be continuously varied, find the relation between n_(1) ,n_(2) R and r for which the current in R in maximum.

Explanation

To solve the problem step by step, we will break it down into two parts as per the question.

Part (a): Finding the current in the external resistance R

1. Understanding the Configuration:
- We have `n1` cells connected in series. The total emf from these cells is:
\( V_{AB} = n1 \cdot \epsilon \)
- Each cell has an internal resistance `r`, so the total internal resistance of the series combination is:
\( R_{series} = n1 \cdot r \)

2. Finding the Equivalent Resistance of the Parallel Combination:
- Since there are `n2` such series combinations connected in parallel, the equivalent resistance of this parallel combination can be calculated using the formula for parallel resistances:
\( \frac{1}{R_{eq}} = \frac{1}{R_{series}} + \frac{1}{R_{series}} + \ldots \text{(n2 times)} \)
- This simplifies to:
\( R_{eq} = \frac{R_{series}}{n2} = \frac{n1 \cdot r}{n2} \)

3. Total Resistance in the Circuit:
- The total resistance in the circuit, which includes the external resistance `R`, is:
\( R_{total} = R_{eq} + R = \frac{n1 \cdot r}{n2} + R \)

4. Calculating the Current:
- Using Ohm's Law, the current `I` flowing through the external resistance `R` can be calculated as:
\( I = \frac{V_{AB}}{R_{total}} = \frac{n1 \cdot \epsilon}{\frac{n1 \cdot r}{n2} + R} \)
- Simplifying this gives:
\( I = \frac{n1 \cdot n2 \cdot \epsilon}{n1 \cdot r + n2 \cdot R} \)

Part (b): Finding the relation for maximum current

1. Condition for Maximum Current:
- To maximize the current `I`, we need to minimize the denominator of the current equation:
\( n1 \cdot r + n2 \cdot R \)

2. Using the Method of Lagrange Multipliers:
- We can set up the condition for maximum current by differentiating with respect to `n1` and `n2` and setting the derivative to zero. However, a simpler approach is to realize that for maximum current:
\( n1 \cdot r = n2 \cdot R \)

3. Final Relation:
- Rearranging gives us the desired relationship:
\( \frac{n1}{n2} = \frac{R}{r} \)

Summary of Results
- Current in External Resistance:
\( I = \frac{n1 \cdot n2 \cdot \epsilon}{n1 \cdot r + n2 \cdot R} \)
- Condition for Maximum Current:
\( n1 \cdot r = n2 \cdot R \)