A wire of resistance 15.0(Ω)is bent to form a regular hexagon ABCDEFA.Find the equivalent resistance of the loop between the points (a)A and B, (b)A and C and (c )A and D .
To solve the problem of finding the equivalent resistance of a wire bent into a regular hexagon, we will follow these steps:
Step 1: Determine the Resistance of Each Side
The total resistance of the wire is given as R=15.0Ω. Since the wire is bent into a regular hexagon, it has 6 equal sides. Therefore, the resistance of each side of the hexagon can be calculated as:
Rside=R6=15.0Ω6=2.5Ω
Step 2: Find the Equivalent Resistance between Points A and B
To find the equivalent resistance between points A and B:
- The resistance between A and B is RAB=Rside=2.5Ω.
- The other 5 sides (C, D, E, F, A) are in series, giving a total resistance of:
R′=5×Rside=5×2.5Ω=12.5Ω
- Now, we have RAB in parallel with R′:
Req, AB=RAB×R′RAB+R′=2.5Ω×12.5Ω2.5Ω+12.5Ω
Calculating this gives:
Req, AB=31.2515=2.0833Ω≈2.08Ω
Step 3: Find the Equivalent Resistance between Points A and C
For points A and C:
- The resistance from A to C includes two sides in series (A to B and B to C):
RAC=2×Rside=2×2.5Ω=5.0Ω
- The remaining four sides (D, E, F, A) are in series:
R′=4×Rside=4×2.5Ω=10.0Ω
- Now, we have RAC in parallel with R′:
Req, AC=RAC×R′RAC+R′=5.0Ω×10.0Ω5.0Ω+10.0Ω
Calculating this gives:
Req, AC=5015=3.3333Ω≈3.33Ω
Step 4: Find the Equivalent Resistance between Points A and D
For points A and D:
- The resistance from A to D includes three sides in series:
RAD=3×Rside=3×2.5Ω=7.5Ω
- The remaining three sides (B, C, A) are also in series:
R′=3×Rside=3×2.5Ω=7.5Ω
- Now, we have RAD in parallel with R′:
Req, AD=RAD×R′RAD+R′=7.5Ω×7.5Ω7.5Ω+7.5Ω
Calculating this gives:
Req, AD=56.2515=3.75Ω
Final Results
- Req, AB=2.08Ω
- Req, AC=3.33Ω
- Req, AD=3.75Ω
The total resistance of the wire is given as R=15.0Ω. Since the wire is bent into a regular hexagon, it has 6 equal sides. Therefore, the resistance of each side of the hexagon can be calculated as:
Rside=R6=15.0Ω6=2.5Ω
To find the equivalent resistance between points A and B:
- The resistance between A and B is RAB=Rside=2.5Ω.
- The other 5 sides (C, D, E, F, A) are in series, giving a total resistance of:
R′=5×Rside=5×2.5Ω=12.5Ω
- Now, we have RAB in parallel with R′:
Req, AB=RAB×R′RAB+R′=2.5Ω×12.5Ω2.5Ω+12.5Ω
Calculating this gives:
Req, AB=31.2515=2.0833Ω≈2.08Ω
For points A and C:
- The resistance from A to C includes two sides in series (A to B and B to C):
RAC=2×Rside=2×2.5Ω=5.0Ω
- The remaining four sides (D, E, F, A) are in series:
R′=4×Rside=4×2.5Ω=10.0Ω
- Now, we have RAC in parallel with R′:
Req, AC=RAC×R′RAC+R′=5.0Ω×10.0Ω5.0Ω+10.0Ω
Calculating this gives:
Req, AC=5015=3.3333Ω≈3.33Ω
For points A and D:
- The resistance from A to D includes three sides in series:
RAD=3×Rside=3×2.5Ω=7.5Ω
- The remaining three sides (B, C, A) are also in series:
R′=3×Rside=3×2.5Ω=7.5Ω
- Now, we have RAD in parallel with R′:
Req, AD=RAD×R′RAD+R′=7.5Ω×7.5Ω7.5Ω+7.5Ω
Calculating this gives:
Req, AD=56.2515=3.75Ω
- Req, AB=2.08Ω
- Req, AC=3.33Ω
- Req, AD=3.75Ω
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT IN CONDUCTORSExercise:questions for short answer
Explore 17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT IN CONDUCTORSExercise:objective 2
Explore 9 Videos
- DISPERSION AND SPECTRABook:HC VERMA ENGLISHChapter:DISPERSION AND SPECTRAExercise:Question for short Answer
Explore 6 Videos
- ELECTRIC CURRENT THROUGH GASESBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT THROUGH GASESExercise:Short answer
Explore 6 Videos
Similar Questions
Knowledge Check
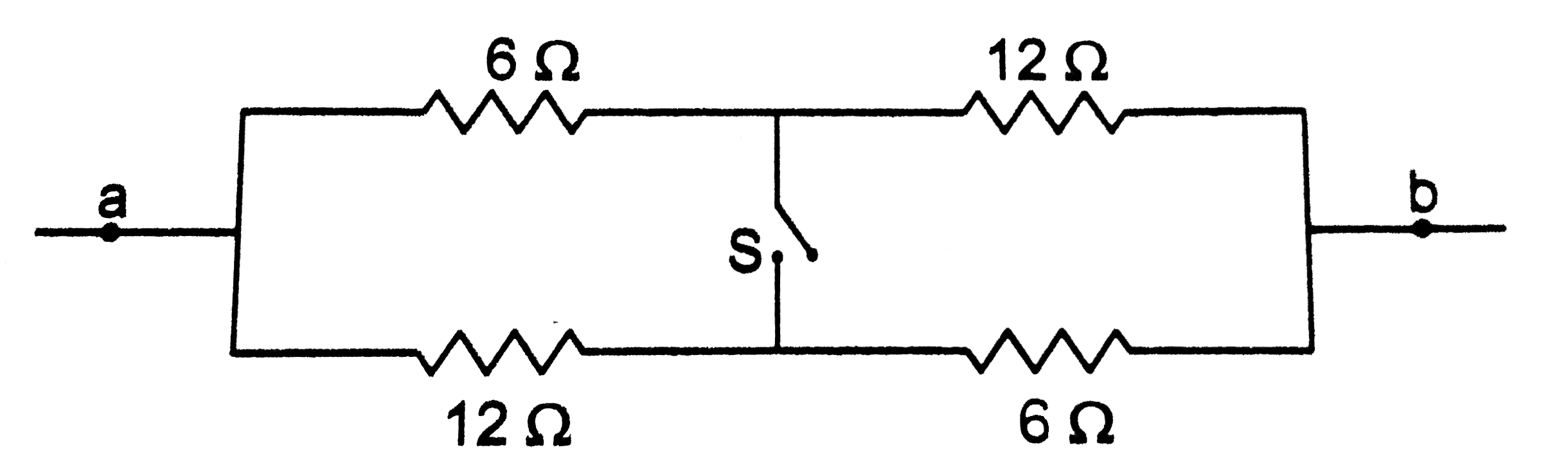
Equivalent resistance of the given network between points A and B is
 A31/5ΩB41/5ΩC36/5ΩD49/5Ω
A31/5ΩB41/5ΩC36/5ΩD49/5Ω
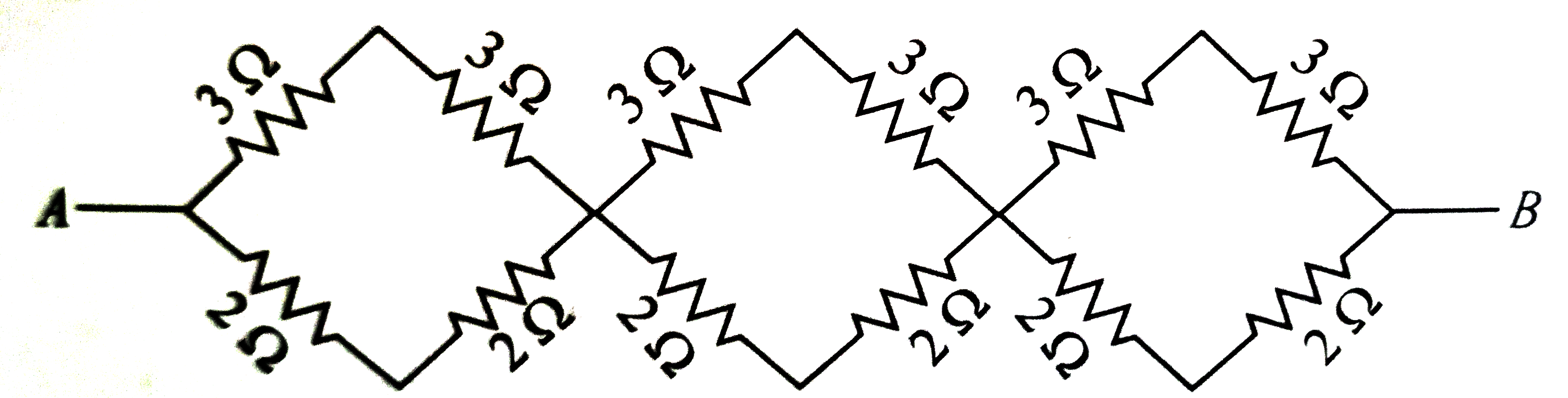
The equivalent resistance between the points A and B is:
View SolutionFind the equivalent resistance between A and B

View SolutionFind the equivalent resistance between A and B
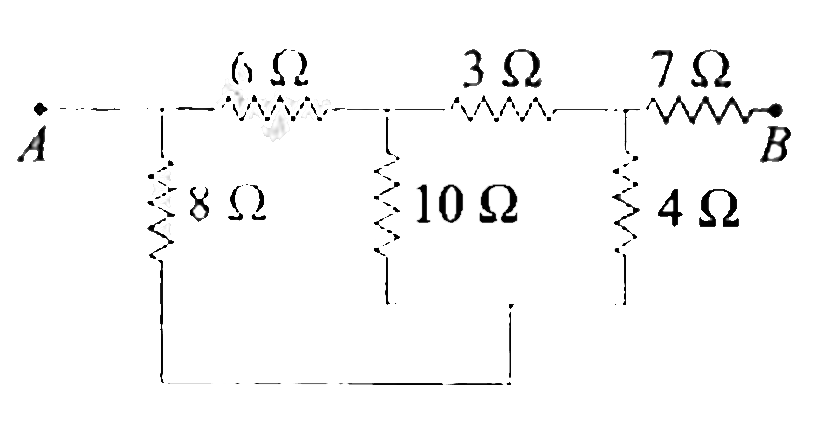
View SolutionFind the equivalent resistance of the network shown in figure between the points A and B .
View SolutionFind the equivalent resistance of the triangular bipyramid between the points.

a. A and C , b. DandE
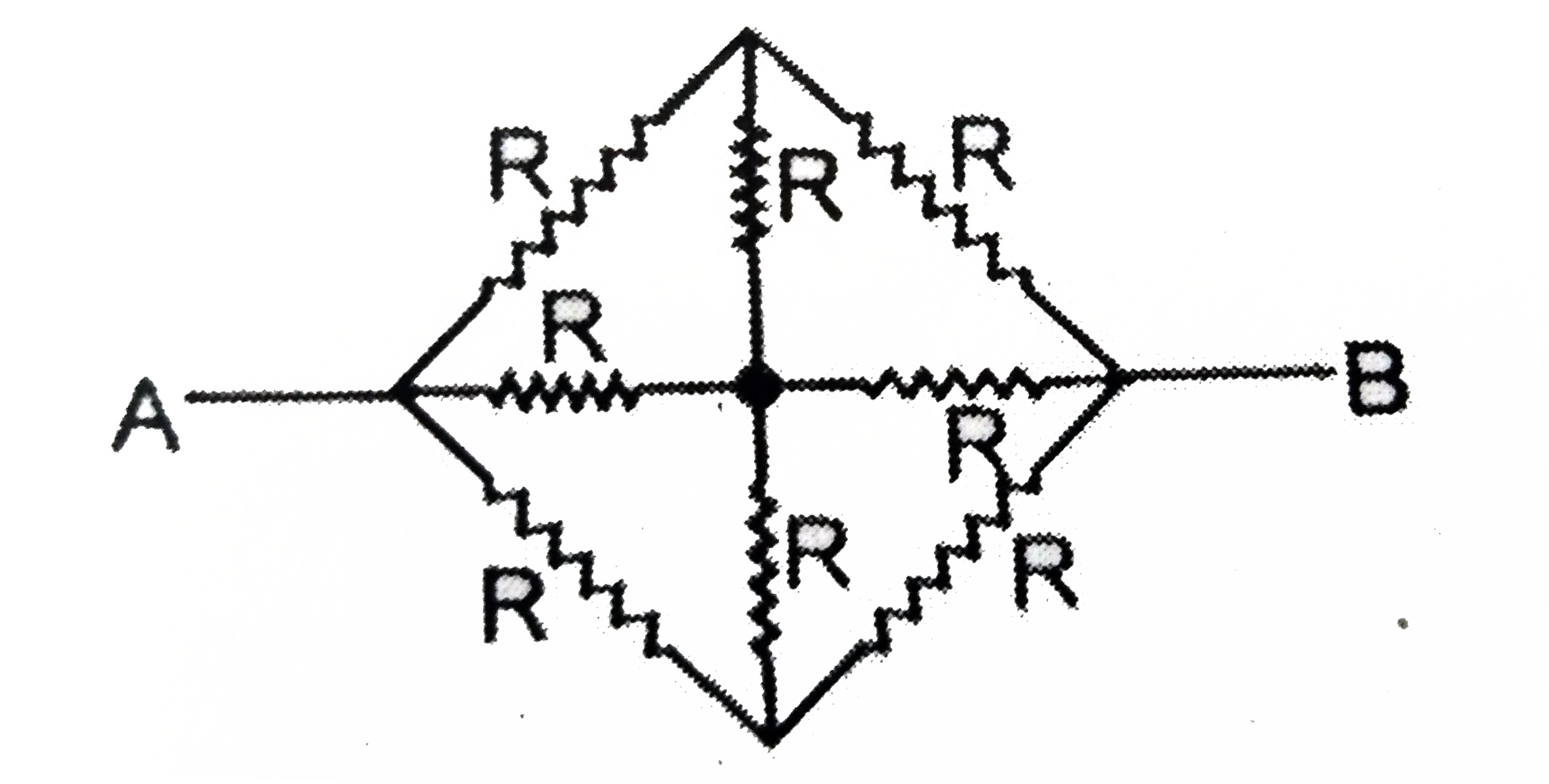
View SolutionFind the equivalent resistance between points A and B

View SolutionEquivalent resistance between the points A and B (in Ω)
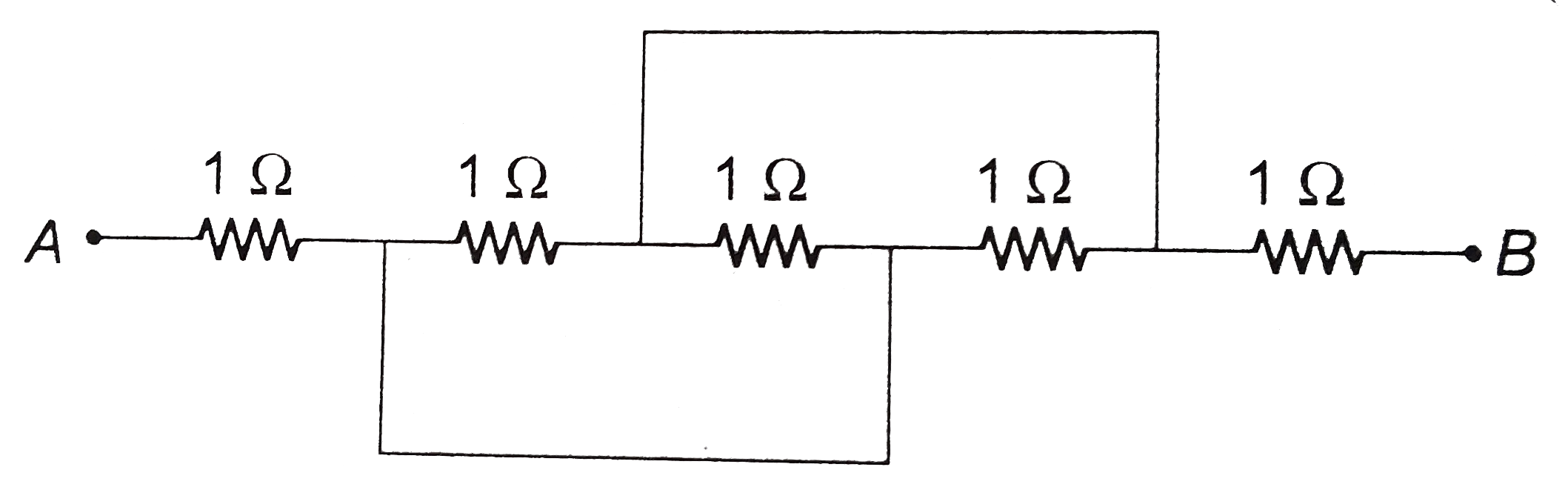 .
.
View Solution