In a arrangement, 3n cells of emf ε and internal resistance r are connected in series. Out of 3n cells polarity of n cells is reversed. Current in the circuit is

2εlor
2ε3r
ε3r
εr
The correct Answer is:C
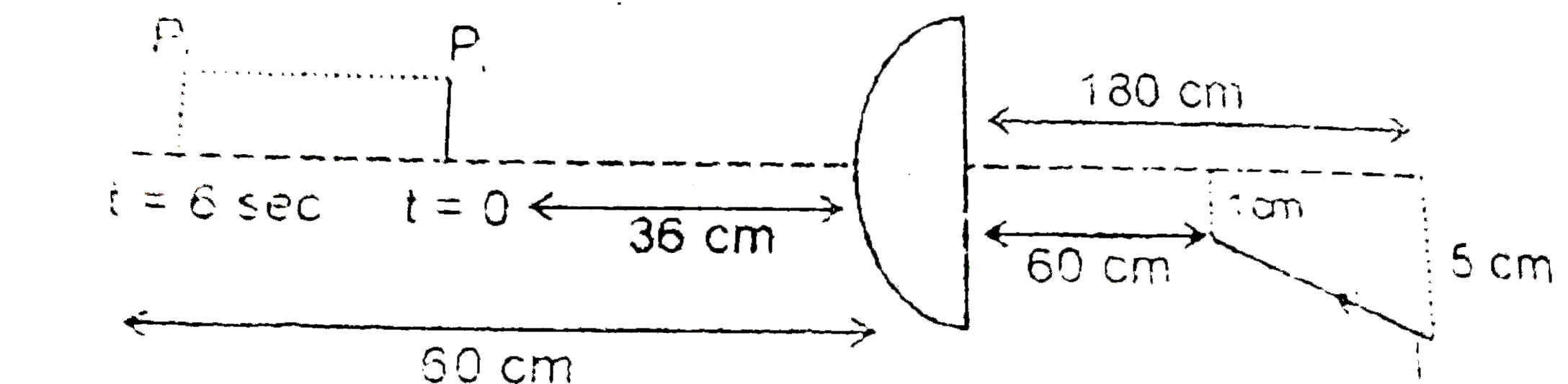
1f=(32−1)(115)
f=30 cm
1v+136=130⇒1v=130−136=1180
v=180 cm.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.39
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.40
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.37
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A cell of emf ε and internal resistance r is charged by a current I, then
View SolutionTen cells each of emf 1V and internal resistance 1Ω are connected inseries. In this arrangement, polarity of two cells is reversed and the system is connected to an external resistance of 2Ω. Find the current in the circuit.
View Solution
Knowledge Check
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
Four identical cells of emf ε and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
View SolutionN identical cells, each of emf ε and internal resistances r are joined in series. Out of these, n cells are wrongly connected, i.e. their terminals are connected in reverse order as required for series connection. If εo be the emf of the resulting battery and ro be its internal resistance then for n <N/2
View Solutionn identical cells, each of emf ε and internal resistance r, are joined in series to form a closed cirucit. One cell A is joined with reversed polarity. The potential difference across any one cell is
View SolutionThree identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View Solutionn identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View Solution
