Ten cells each of emf 1V and internal resistance 1Ω are connected inseries. In this arrangement, polarity of two cells is reversed and the system is connected to an external resistance of 2Ω. Find the current in the circuit.
The correct Answer is:A, B
To solve the problem step by step, we will analyze the circuit with the given parameters.
Step 1: Identify the parameters
We have:
- Number of cells, n=10
- EMF of each cell, E=1V
- Internal resistance of each cell, r=1Ω
- External resistance, R=2Ω
- Two cells have their polarity reversed.
Step 2: Calculate the total EMF
When two cells have their polarity reversed, they effectively subtract their EMF from the total. Therefore, the total EMF can be calculated as follows:
Total EMF=(n−2)⋅E=(10−2)⋅1=8V
So, the effective EMF after reversing the polarity of two cells is:
Eequiv=8V−2V=6V
Step 3: Calculate the total internal resistance
Since all cells are in series, the total internal resistance can be calculated as:
Rinternal=n⋅r=10⋅1=10Ω
Step 4: Calculate the total resistance in the circuit
The total resistance in the circuit is the sum of the internal resistance and the external resistance:
Rtotal=Rinternal+R=10Ω+2Ω=12Ω
Step 5: Calculate the current in the circuit
Using Ohm's law, the current I in the circuit can be calculated using the formula:
I=EequivRtotal=6V12Ω=12A
Final Answer
The current in the circuit is I=0.5A.
---
We have:
- Number of cells, n=10
- EMF of each cell, E=1V
- Internal resistance of each cell, r=1Ω
- External resistance, R=2Ω
- Two cells have their polarity reversed.
When two cells have their polarity reversed, they effectively subtract their EMF from the total. Therefore, the total EMF can be calculated as follows:
Since all cells are in series, the total internal resistance can be calculated as:
The total resistance in the circuit is the sum of the internal resistance and the external resistance:
Using Ohm's law, the current I in the circuit can be calculated using the formula:
The current in the circuit is I=0.5A.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise 23.7
Explore 1 Video
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise 23.8
Explore 3 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise 23.5
Explore 2 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
Similar Questions
24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionIn a arrangement, 3n cells of emf ε and internal resistance r are connected in series. Out of 3n cells polarity of n cells is reversed. Current in the circuit is

View SolutionThree identical cells each of emf 2 V and internal resistance 1Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6Ω Find the current delivered by the battery.
View SolutionThree identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionThere are n cells, each of emf E and internal resistance r, connected in series with an external resistance R. One of the cells is wrongly connected, so that it sends current in the opposite direction. The current flowing in the circuit is
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of 1Ω and 2Ω respectively, are connected in parallel so as to read the current in the same direction through an external resistance of 5Ω . The current in the external resistance will be
View SolutionEight cells marked 1 to 8, each of emf 5V and internal resistance 0.2Ω are connected as shown. What is the reading of ideal voltmeter ?
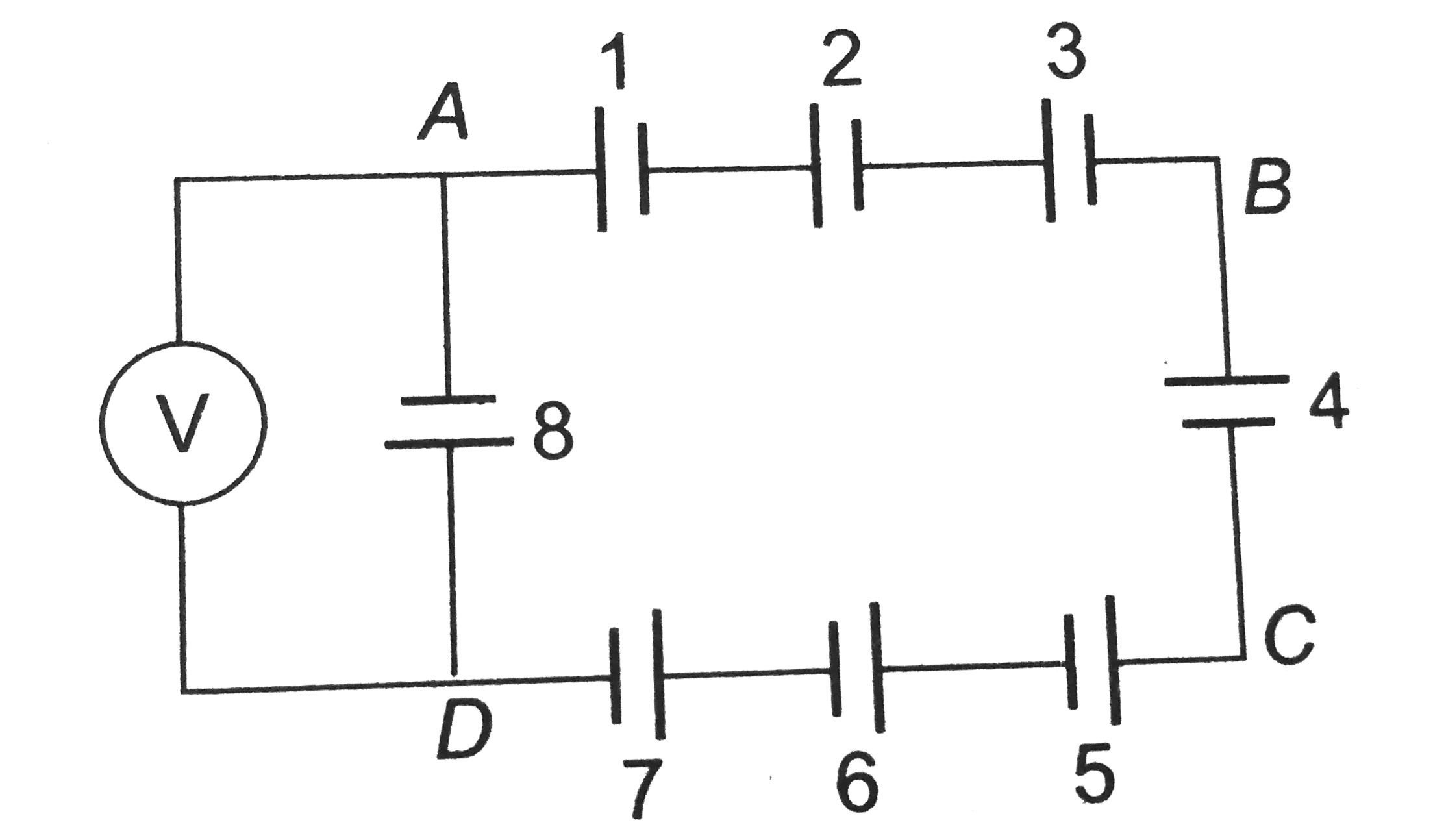
View SolutionA battery of 10 cells each of e.m.f. E=1.5V and internal resistance 0.5Ω has 1 cell wrongly connected. It is being charged by 220V power supply with an external resistance of 47Ω in series. The potential difference across the battery.
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
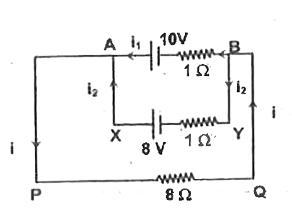
View Solution

