A battery of 10 cells each of e.m.f. E=1.5V and internal resistance 0.5Ω has 1 cell wrongly connected. It is being charged by 220V power supply with an external resistance of 47Ω in series. The potential difference across the battery.
2Av
2Av2
2Av12
Can't be determined
The correct Answer is:(B)
To solve the problem, we will follow these steps:
Step 1: Calculate the total EMF of the battery
Since one cell is wrongly connected, we have 9 cells connected correctly. The EMF of each cell is given as E=1.5V.
Total EMF=9×E=9×1.5=13.5V
Step 2: Calculate the total internal resistance of the battery
The internal resistance of each cell is given as r=0.5Ω. Since one cell is wrongly connected, we have 9 cells contributing to the internal resistance.
Total Internal Resistance=9×r=9×0.5=4.5Ω
Step 3: Calculate the total resistance in the circuit
The external resistance Rext is given as 47Ω. The total resistance in the circuit Rtotal is the sum of the external resistance and the internal resistance of the battery.
Rtotal=Rext+Rinternal=47+4.5=51.5Ω
Step 4: Calculate the total voltage supplied by the power supply
The voltage supplied by the power supply is Vsupply=220V.
Step 5: Calculate the current flowing through the circuit
Using Ohm's law, the current I can be calculated as:
I=VsupplyRtotal=22051.5≈4.27A
Step 6: Calculate the potential difference across the battery
The potential difference V across the battery can be calculated using the formula:
V=Total EMF−I×Rinternal
Substituting the values we have:
V=13.5−(4.27×4.5)≈13.5−19.215≈−5.715V
Since the potential difference is negative, it indicates that the battery is being charged in reverse due to the wrongly connected cell.
Final Answer
The potential difference across the battery is approximately −5.715V.
---
Since one cell is wrongly connected, we have 9 cells connected correctly. The EMF of each cell is given as E=1.5V.
The internal resistance of each cell is given as r=0.5Ω. Since one cell is wrongly connected, we have 9 cells contributing to the internal resistance.
The external resistance Rext is given as 47Ω. The total resistance in the circuit Rtotal is the sum of the external resistance and the internal resistance of the battery.
The voltage supplied by the power supply is Vsupply=220V.
Using Ohm's law, the current I can be calculated as:
The potential difference V across the battery can be calculated using the formula:
The potential difference across the battery is approximately −5.715V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EXERCISE-III
Explore 26 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EXERCISE-IV A
Explore 32 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE (J-A)
Explore 6 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
Similar Questions
A battery of six cells each of e.m.f . 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω. What is the potential difference across the battery?
View SolutionA battery of six cells each of e.m.f. 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω what will be the charging current.
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig. What is the potential difference across the terminals of the cell ?
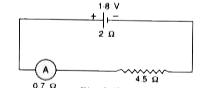
View SolutionA battery of 20 cells (each having e.m.f. 1.8V and internal resistance 0.1Ω is charged by 220 volts and the charging current is 15A. Calculate the resistance to be put in the circuit.
View SolutionA battery of e.m.f. 12 V and internal resistance 2 Ω is connected with two resistors A and B of resistance 4 Ω and 6 Ω respectively joined in series.
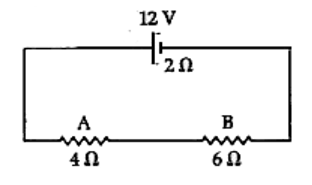
Find The potential difference across 6 Ω Resistor.
View SolutionA cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in Fig.
find : the potential difference across the 4.5 Ω resistor.
View SolutionTen cells each of emf 1V and internal resistance 1Ω are connected inseries. In this arrangement, polarity of two cells is reversed and the system is connected to an external resistance of 2Ω. Find the current in the circuit.
View SolutionTwo batteries of e.m.f. 4V and 8V with internal resistances 1Ω and 2Ω are connected in a circuit with a resistance of 9Ω as shown in figure. The current and potential difference between the points P and Q
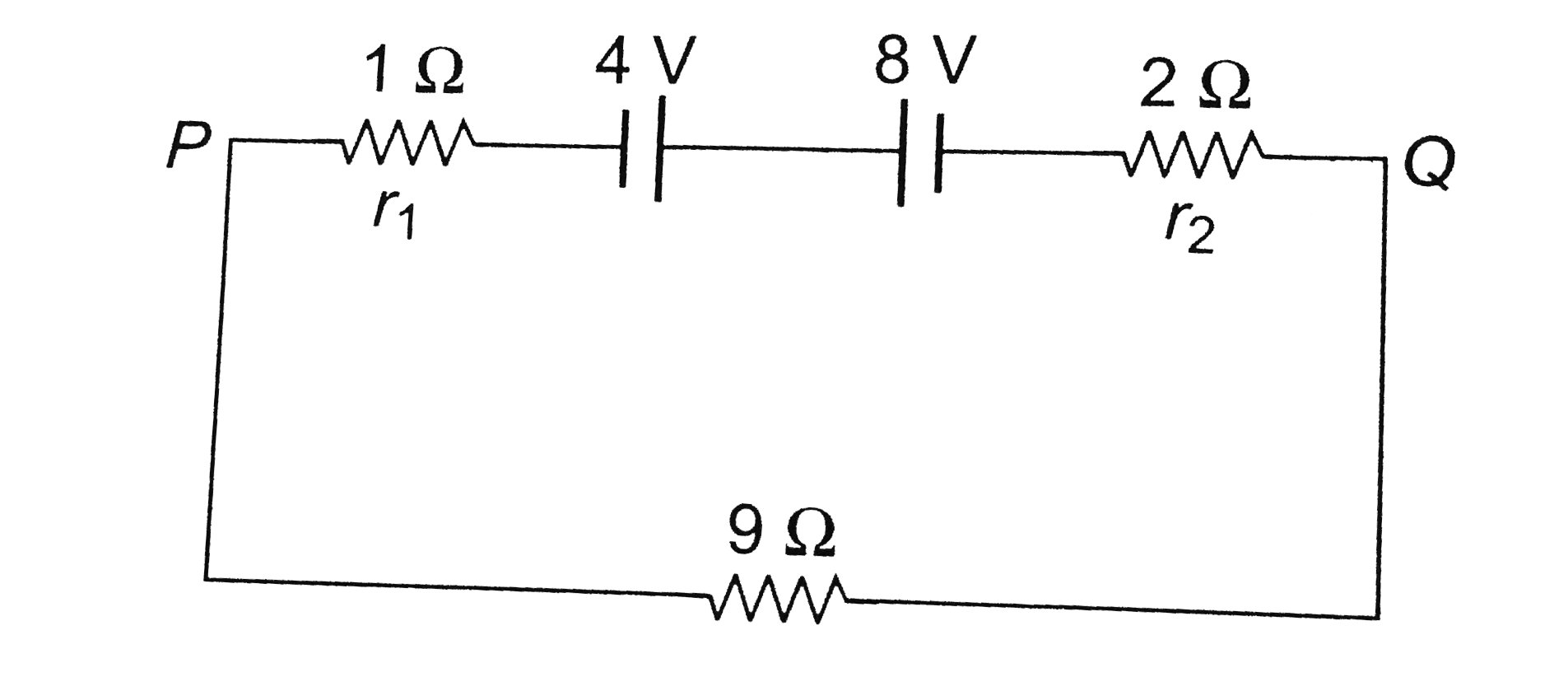
View SolutionA set of 4 cell each of emf 2V and internal resistance 1.5Ω are connected across an external load of 10Ω with 2 rows, two cells in each row. Calculate the current in each row and potential difference across 10Ω
View Solution