24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
in order to send the maximum current through a 12Ω resistor, connect the two rows of 12 cells in series
the current is each row is 0.375A
the current in each cell is 0.75A
potential difference across 12Ω resistor is 4.5V
The correct Answer is:A, B
To solve the problem step by step, we will analyze the given data and apply the relevant formulas.
Step 1: Identify Given Data
- Number of cells (N) = 24
- EMF of each cell (E) = 1.5 V
- Internal resistance of each cell (r) = 2 Ω
- External resistance (R) = 12 Ω
Step 2: Determine Configuration of Cells
We need to connect the cells in such a way that we maximize the current through the external resistor. We can assume that the cells are arranged in m rows and n columns.
From the problem, we know:
- Total number of cells = m × n = 24 (Equation 1)
- For maximum current, the condition is R = n × r/m, where R is the external resistance, r is the internal resistance of each cell, and n is the number of cells in series in each row.
Step 3: Set Up the Equation for Maximum Current
From the condition for maximum current:
\( R = \frac{n \cdot r}{m} \)
Substituting the values:
\( 12 = \frac{n \cdot 2}{m} \)
This simplifies to:
\( n = 6m \) (Equation 2)
Step 4: Solve the Equations
Now we have two equations:
1. \( m \cdot n = 24 \) (Equation 1)
2. \( n = 6m \) (Equation 2)
Substituting Equation 2 into Equation 1:
\( m \cdot (6m) = 24 \)
\( 6m^2 = 24 \)
\( m^2 = 4 \)
\( m = 2 \)
Now substituting back to find n:
\( n = 6 \cdot 2 = 12 \)
Step 5: Configuration of Cells
Thus, we have:
- m = 2 (rows)
- n = 12 (columns)
This means we have 2 rows of 12 cells connected in parallel.
Step 6: Calculate Maximum Current
The maximum current through the external resistance can be calculated using the formula:
\( I_{max} = \frac{m \cdot E}{R + (n \cdot r)} \)
Substituting the values:
\( I_{max} = \frac{2 \cdot 1.5}{12 + (12 \cdot 2)} \)
\( I_{max} = \frac{3}{12 + 24} \)
\( I_{max} = \frac{3}{36} \)
\( I_{max} = 0.0833 \, \text{A} \)
Step 7: Calculate Current in Each Row
Since the rows are in parallel, the current in each row can be calculated as:
\( I_{row} = \frac{I_{max}}{m} = \frac{0.0833}{2} = 0.04165 \, \text{A} \)
Step 8: Calculate Potential Difference Across External Resistance
The potential difference across the external resistance can be calculated as:
\( V = I_{max} \cdot R = 0.0833 \cdot 12 = 1 \, \text{V} \)
Summary of Results
1. The configuration for maximum current is 2 rows of 12 cells each.
2. The current in each row is approximately 0.04165 A.
3. The potential difference across the 12 Ω resistor is 1 V.
- Number of cells (N) = 24
- EMF of each cell (E) = 1.5 V
- Internal resistance of each cell (r) = 2 Ω
- External resistance (R) = 12 Ω
We need to connect the cells in such a way that we maximize the current through the external resistor. We can assume that the cells are arranged in m rows and n columns.
- Total number of cells = m × n = 24 (Equation 1)
- For maximum current, the condition is R = n × r/m, where R is the external resistance, r is the internal resistance of each cell, and n is the number of cells in series in each row.
From the condition for maximum current:
\( R = \frac{n \cdot r}{m} \)
Substituting the values:
\( 12 = \frac{n \cdot 2}{m} \)
This simplifies to:
\( n = 6m \) (Equation 2)
Now we have two equations:
1. \( m \cdot n = 24 \) (Equation 1)
2. \( n = 6m \) (Equation 2)
\( m \cdot (6m) = 24 \)
\( 6m^2 = 24 \)
\( m^2 = 4 \)
\( m = 2 \)
\( n = 6 \cdot 2 = 12 \)
Thus, we have:
- m = 2 (rows)
- n = 12 (columns)
The maximum current through the external resistance can be calculated using the formula:
\( I_{max} = \frac{m \cdot E}{R + (n \cdot r)} \)
Substituting the values:
\( I_{max} = \frac{2 \cdot 1.5}{12 + (12 \cdot 2)} \)
\( I_{max} = \frac{3}{12 + 24} \)
\( I_{max} = \frac{3}{36} \)
\( I_{max} = 0.0833 \, \text{A} \)
Since the rows are in parallel, the current in each row can be calculated as:
\( I_{row} = \frac{I_{max}}{m} = \frac{0.0833}{2} = 0.04165 \, \text{A} \)
The potential difference across the external resistance can be calculated as:
\( V = I_{max} \cdot R = 0.0833 \cdot 12 = 1 \, \text{V} \)
1. The configuration for maximum current is 2 rows of 12 cells each.
2. The current in each row is approximately 0.04165 A.
3. The potential difference across the 12 Ω resistor is 1 V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - III LEVEL-II (ADVANCED) (Linked Comprehension Type Questions))
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - III LEVEL-II (ADVANCED) (Matching Type Questions))
1 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE SHEET (EXERCISE - III LEVEL-I (MAIN) (Straight Objective Type Questions))
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
Three identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View Solution24 cells of emf 1.5V each having internal resistance of 1 ohm are connected to an external resistance of 1.5 ohms. To get maximum current,
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
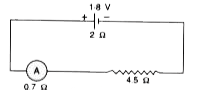
What would be the reading of the ammeter ?
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig. What is the potential difference across the terminals of the cell ?
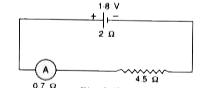
View SolutionThree identical cells each of emf 2 V and internal resistance 1Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6Ω Find the current delivered by the battery.
View SolutionA battery of 24 cells each of emf 1.5 V and internal resistnace 2Ω is to be connected in order to send the maximum current through a 12Ω resistor. The correct arrangement of cells will be
View SolutionTwo batteries, one of emf 18V and internal resistance 2Ω and the other of emf 12 and internal resistance 1Ω , are connected as shown. The voltmeter V will record a reading of

View SolutionIf three uniform spheres, each having mass M and radius R, are kept in such a way that each touches the other two, the magnitude of the gravitational force on any sphere due to the other two is:
View SolutionA set of 4 cell each of emf 2V and internal resistance 1.5Ω are connected across an external load of 10Ω with 2 rows, two cells in each row. Calculate the current in each row and potential difference across 10Ω
View Solution
