n identical cells, each of emf ε and internal resistance r, are joined in series to form a closed cirucit. One cell A is joined with reversed polarity. The potential difference across any one cell is
zero
ε
2εn
n−1nε
The correct Answer is:A
To solve the problem step by step, we need to analyze the circuit formed by the n identical cells, each with an emf (ε) and internal resistance (r), where one cell is connected with reversed polarity.
Step 1: Determine the total emf in the circuit
When n identical cells are connected in series, the total emf (E_net) can be calculated by considering the effect of the reversed cell. If one cell is connected in reverse, it subtracts its emf from the total.
For n cells, if one cell is reversed, the total emf can be expressed as:
Enet=(n−1)ϵ−ϵ=(n−2)ϵ
Step 2: Calculate the total internal resistance
The total internal resistance (R_net) of n cells connected in series is simply the sum of the internal resistances of each cell:
Rnet=n⋅r
Step 3: Find the current in the circuit
Using Ohm's law, the current (I) flowing through the circuit can be calculated as:
I=EnetRnet=(n−2)ϵn⋅r
Step 4: Calculate the potential difference across one cell
The potential difference (V) across one cell can be calculated using the formula:
V=ϵ−I⋅r
Substituting the value of I from Step 3:
V=ϵ−((n−2)ϵn⋅r)⋅r
Step 5: Simplify the expression for V
Now, simplifying the expression:
V=ϵ−(n−2)ϵn
V=ϵ(1−(n−2)n)
V=ϵ(n−(n−2)n)
V=ϵ(2n)
Final Result
Thus, the potential difference across one cell is:
V=2ϵn
When n identical cells are connected in series, the total emf (E_net) can be calculated by considering the effect of the reversed cell. If one cell is connected in reverse, it subtracts its emf from the total.
Enet=(n−1)ϵ−ϵ=(n−2)ϵ
The total internal resistance (R_net) of n cells connected in series is simply the sum of the internal resistances of each cell:
Rnet=n⋅r
Using Ohm's law, the current (I) flowing through the circuit can be calculated as:
I=EnetRnet=(n−2)ϵn⋅r
The potential difference (V) across one cell can be calculated using the formula:
V=ϵ−I⋅r
Substituting the value of I from Step 3:
V=ϵ−((n−2)ϵn⋅r)⋅r
Now, simplifying the expression:
V=ϵ−(n−2)ϵn
V=ϵ(1−(n−2)n)
V=ϵ(n−(n−2)n)
V=ϵ(2n)
Thus, the potential difference across one cell is:
V=2ϵn
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Comprehension
35 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
n identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View Solutionn identical cells, each of emf E and internal resistance r, are joined in series to form a closed circuit. Find the potential difference across any one cell.
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to form a loop. The terminal voltage across each cells is
View SolutionA group of n identical cells each of EMF E and internal resistance r are joined in series to form a loop as shown . The terminal voltage across each cell is
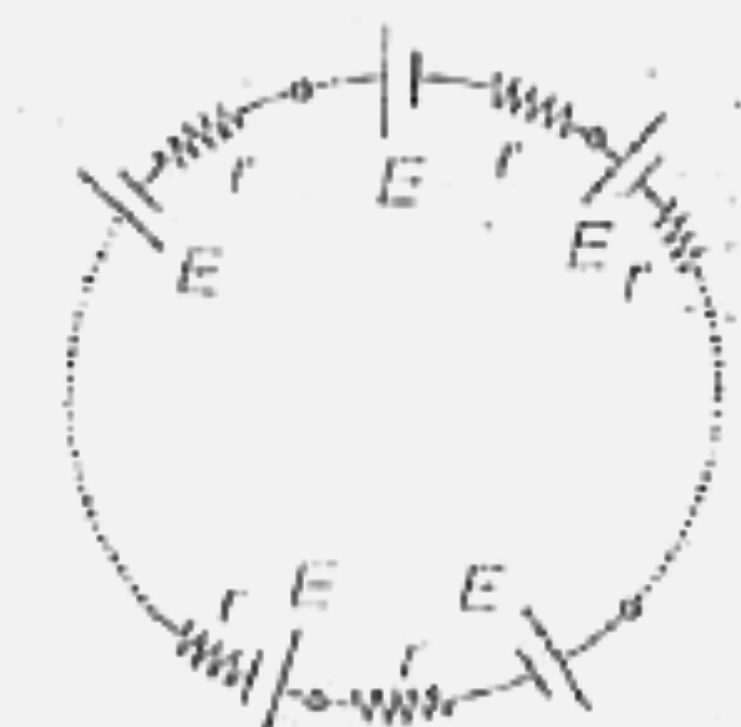
View SolutionN identical cells, each of emf ε and internal resistances r are joined in series. Out of these, n cells are wrongly connected, i.e. their terminals are connected in reverse order as required for series connection. If εo be the emf of the resulting battery and ro be its internal resistance then for n <N/2
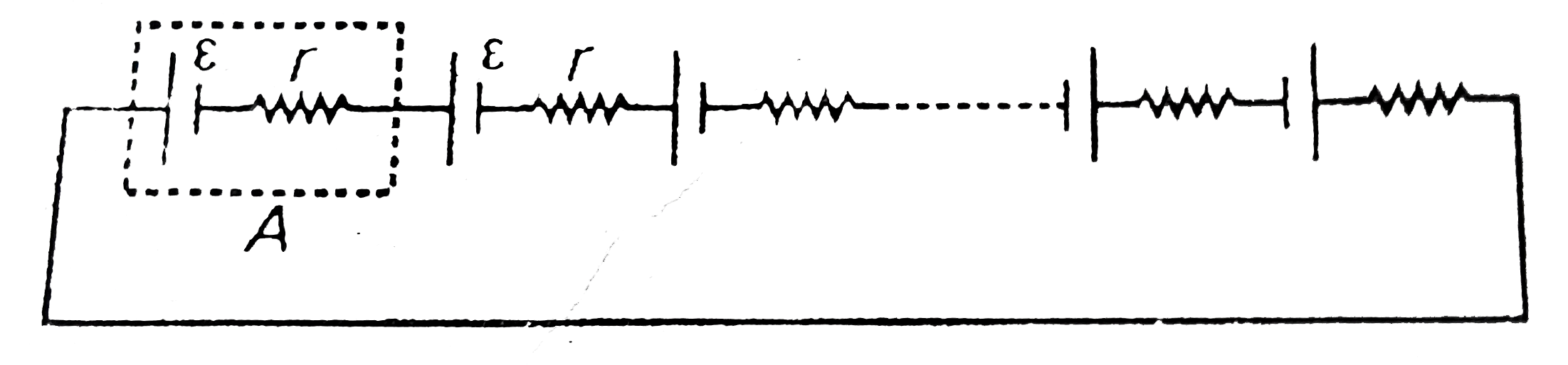
View SolutionIn a arrangement, 3n cells of emf ε and internal resistance r are connected in series. Out of 3n cells polarity of n cells is reversed. Current in the circuit is
View SolutionConsider N=n1n2indentical cells, each of emf(ε) and internal resistance r. Suppose n1 cells are joined in series to forn a line and n_(2) such are connected in parallel. The combination drives a current in an external resistance R.(a) find the current in the external resistance, (b) Assuming that n1and n_(2) can be continuously varied, find the relation between n_(1) ,n_(2) R and r for which the current in R in maximum.
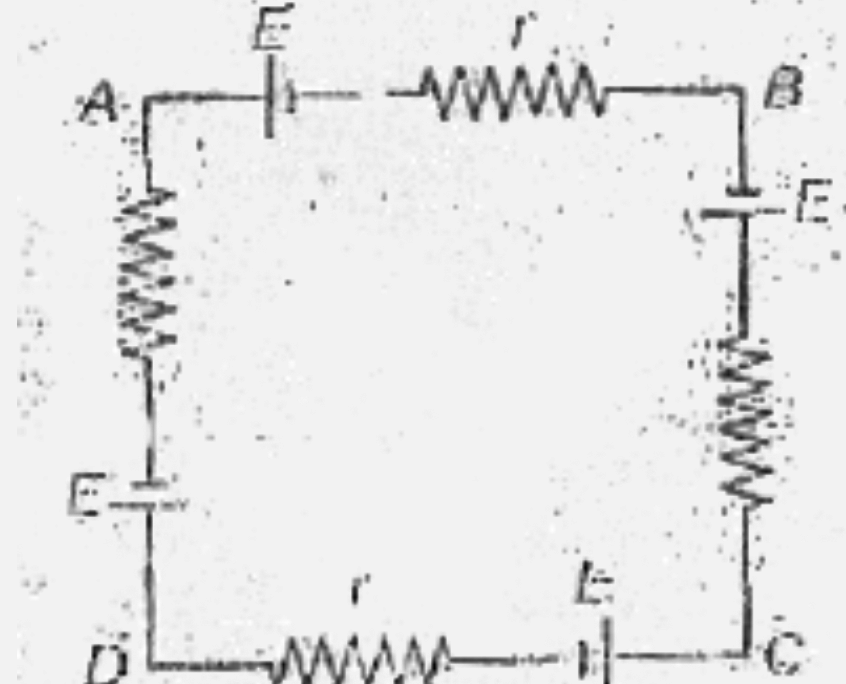
View SolutionFour identical cells each having emf E and internal resistance r are connected in series to form a loop ABCD as shown in figure . Find potential difference across AB and AC .
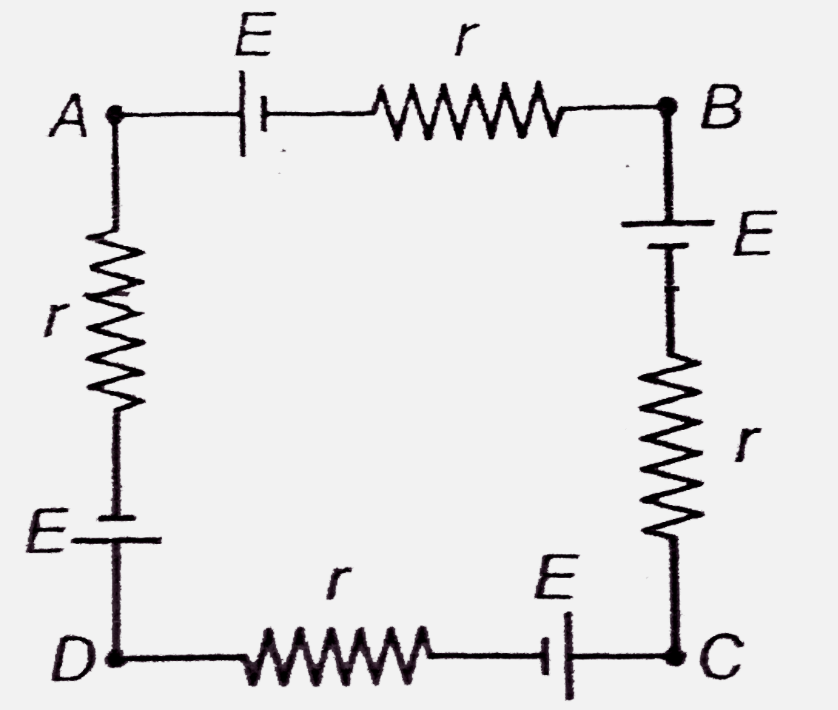
View SolutionFour cells each of emf E and internal resistance r are connected in series to form a loop ABCD. Find potential difference across (1) AB, (2) AC
View Solution
