The emf of a cell is ε and its internal resistance is r. its termnals are cannected to a resistance R. The potential difference between the terminals is 1.6V for R = 4 Omega, and 1.8 V for R = 9 Omega. Then,
ε=1V,r=1Ω
ε=2V,r=1Ω
ε=2V,r=2Ω
ε=2.5V,r=0.5Ω
The correct Answer is:B
To solve the problem, we will use the concepts of electromotive force (emf), internal resistance, and Ohm's law. Let's break down the solution step by step.
Step 1: Write the equations for the two cases
We know that the potential difference (V) across the external resistor (R) can be expressed as:
V=ϵ−I⋅r
Where:
- ϵ is the emf of the cell,
- I is the current flowing through the circuit,
- r is the internal resistance of the cell.
The current I can be calculated using Ohm's law:
I=VR
Step 2: Set up the equations for the two given scenarios
For the first case where R=4Ω and V=1.6V:
1.6=ϵ−I⋅r
Substituting I:
1.6=ϵ−(1.64)r
This simplifies to:
1.6=ϵ−0.4r
Rearranging gives us:
ϵ=1.6+0.4r(Equation 1)
For the second case where R=9Ω and V=1.8V:
1.8=ϵ−I⋅r
Substituting I:
1.8=ϵ−(1.89)r
This simplifies to:
1.8=ϵ−0.2r
Rearranging gives us:
ϵ=1.8+0.2r(Equation 2)
Step 3: Equate the two equations
Since both expressions equal ϵ, we can set them equal to each other:
1.6+0.4r=1.8+0.2r
Step 4: Solve for r
Rearranging the equation:
0.4r−0.2r=1.8−1.6
This simplifies to:
0.2r=0.2
Dividing both sides by 0.2 gives:
r=1Ω
Step 5: Substitute r back to find ϵ
Now we can substitute r=1Ω back into either Equation 1 or Equation 2 to find ϵ. Using Equation 1:
ϵ=1.6+0.4(1)
This simplifies to:
ϵ=1.6+0.4=2.0V
Conclusion
Thus, the values we have found are:
- The emf of the cell ϵ=2.0V
- The internal resistance r=1Ω
We know that the potential difference (V) across the external resistor (R) can be expressed as:
V=ϵ−I⋅r
Where:
- ϵ is the emf of the cell,
- I is the current flowing through the circuit,
- r is the internal resistance of the cell.
I=VR
For the first case where R=4Ω and V=1.6V:
1.6=ϵ−I⋅r
Substituting I:
1.6=ϵ−(1.64)r
This simplifies to:
1.6=ϵ−0.4r
Rearranging gives us:
ϵ=1.6+0.4r(Equation 1)
1.8=ϵ−I⋅r
Substituting I:
1.8=ϵ−(1.89)r
This simplifies to:
1.8=ϵ−0.2r
Rearranging gives us:
ϵ=1.8+0.2r(Equation 2)
Since both expressions equal ϵ, we can set them equal to each other:
1.6+0.4r=1.8+0.2r
Rearranging the equation:
0.4r−0.2r=1.8−1.6
This simplifies to:
0.2r=0.2
Dividing both sides by 0.2 gives:
r=1Ω
Now we can substitute r=1Ω back into either Equation 1 or Equation 2 to find ϵ. Using Equation 1:
ϵ=1.6+0.4(1)
This simplifies to:
ϵ=1.6+0.4=2.0V
Thus, the values we have found are:
- The emf of the cell ϵ=2.0V
- The internal resistance r=1Ω
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Comprehension
35 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
The emf of a cell is ε and its internal resistance is r. its terminals are connected to a resistance R. The potential difference between the terminals is 1.6V for R=4Ω, and 1.8V for R=9Ω. Then,
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionA cell whose e.m.f. is 2V and internal resistance is 0.1Ω is connected with a resistance of 3.9Ω the voltage across the cell terminal will be
View SolutionA cell of emf E is connected across a resistance R. The potential difference between the terminals of the cell is found to be V. The internal resistance of the cell must be -
View SolutionA resistance R is connected across a cell of emf ε and internal resistance r. A potentiometer now measures the potential difference between the terminals of the cell is V. Write the expression for r in terms of ε, V and R.
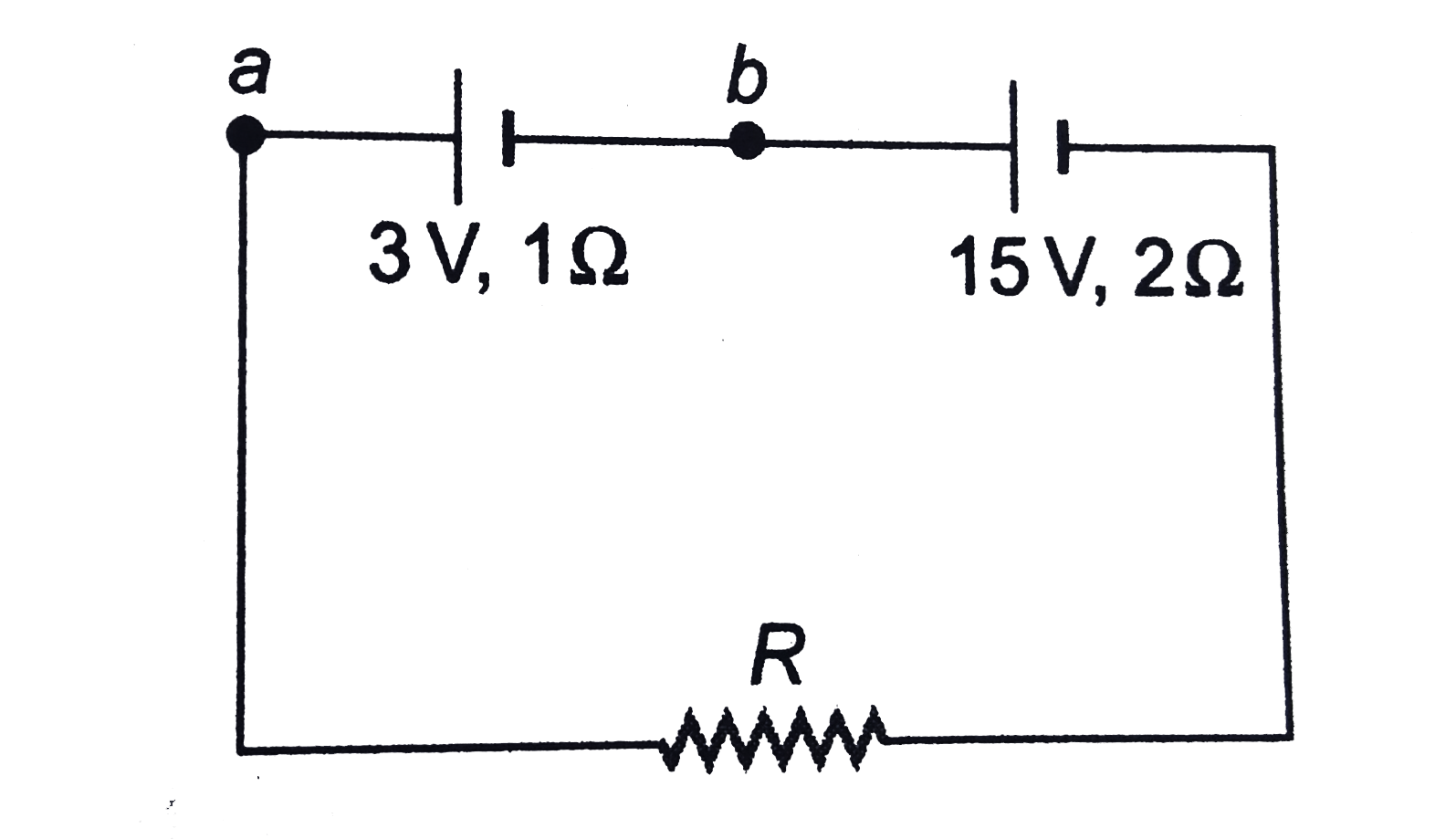
View SolutionTwo batteries one of the emf 3V, internal resistance 1Ω and the other of emf 15V, internal resistance 2Ω are connected in series with a resistance R as shown. If the potential difference between points a and b is zero, the resistance R in Ω is
View SolutionThe emf of a daniel cell is 1.08V. When the terminals of the cell are connected to resistance of 3Ω, the potential difference across the terminals is found to be 0.6 V. Then , the internal resistance of the cell is
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View Solution
