A cell of emf E is connected across a resistance R. The potential difference between the terminals of the cell is found to be V. The internal resistance of the cell must be -
2(E−V)VR
2(E−V)RE
(E−V)RV
(E−V)R
The correct Answer is:C
To solve the problem, we need to find the internal resistance r of a cell given its electromotive force (emf) E, the potential difference V across the terminals, and the external resistance R.
1. Understand the Circuit:
- We have a cell with emf E.
- The cell has an internal resistance r.
- The cell is connected to an external resistance R.
- The potential difference across the terminals of the cell is V.
2. Use Ohm's Law:
- The current I flowing through the circuit can be expressed in two ways:
- From the cell's perspective:
I=Er+R
- From the external resistance's perspective:
I=VR
3. Set the Two Expressions for Current Equal:
- Since both expressions represent the same current I, we can set them equal to each other:
Er+R=VR
4. Cross-Multiply to Eliminate the Fractions:
- Cross-multiplying gives:
E⋅R=V⋅(r+R)
5. Distribute and Rearrange the Equation:
- Distributing V on the right side:
E⋅R=V⋅r+V⋅R
- Rearranging gives:
E⋅R−V⋅R=V⋅r
6. Factor Out R:
- Factoring R from the left side:
R(E−V)=V⋅r
7. Solve for the Internal Resistance r:
- Dividing both sides by V:
r=R(E−V)V
Final Answer:
The internal resistance r of the cell is given by:
r=R(E−V)V
- We have a cell with emf E.
- The cell has an internal resistance r.
- The cell is connected to an external resistance R.
- The potential difference across the terminals of the cell is V.
- The current I flowing through the circuit can be expressed in two ways:
- From the cell's perspective:
I=Er+R
- From the external resistance's perspective:
I=VR
- Since both expressions represent the same current I, we can set them equal to each other:
Er+R=VR
- Cross-multiplying gives:
E⋅R=V⋅(r+R)
- Distributing V on the right side:
E⋅R=V⋅r+V⋅R
- Rearranging gives:
E⋅R−V⋅R=V⋅r
- Factoring R from the left side:
R(E−V)=V⋅r
- Dividing both sides by V:
r=R(E−V)V
The internal resistance r of the cell is given by:
r=R(E−V)V
Topper's Solved these Questions
Similar Questions
A cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionThe emf of a daniel cell is 1.08V. When the terminals of the cell are connected to resistance of 3Ω, the potential difference across the terminals is found to be 0.6 V. Then , the internal resistance of the cell is
View SolutionA cell has an emf 1.5V. When connected across an external resistance of 2Ω, the terminal potential difference falls to 1.0V. The internal resistance of the cell is:
View SolutionA cell which has an emf 1.5 V is connectedin series with an external resistance of 10Ω. If the potential difference across the cell is 1.25 V, then the internal resistance of the cell is (inΩ)
View SolutionFor a cell, a graph is plotted between the potential difference V across the terminals of the cell and the current I drawn the cell. The emf and the internal resistance of the cell are E and r, respectively. Then
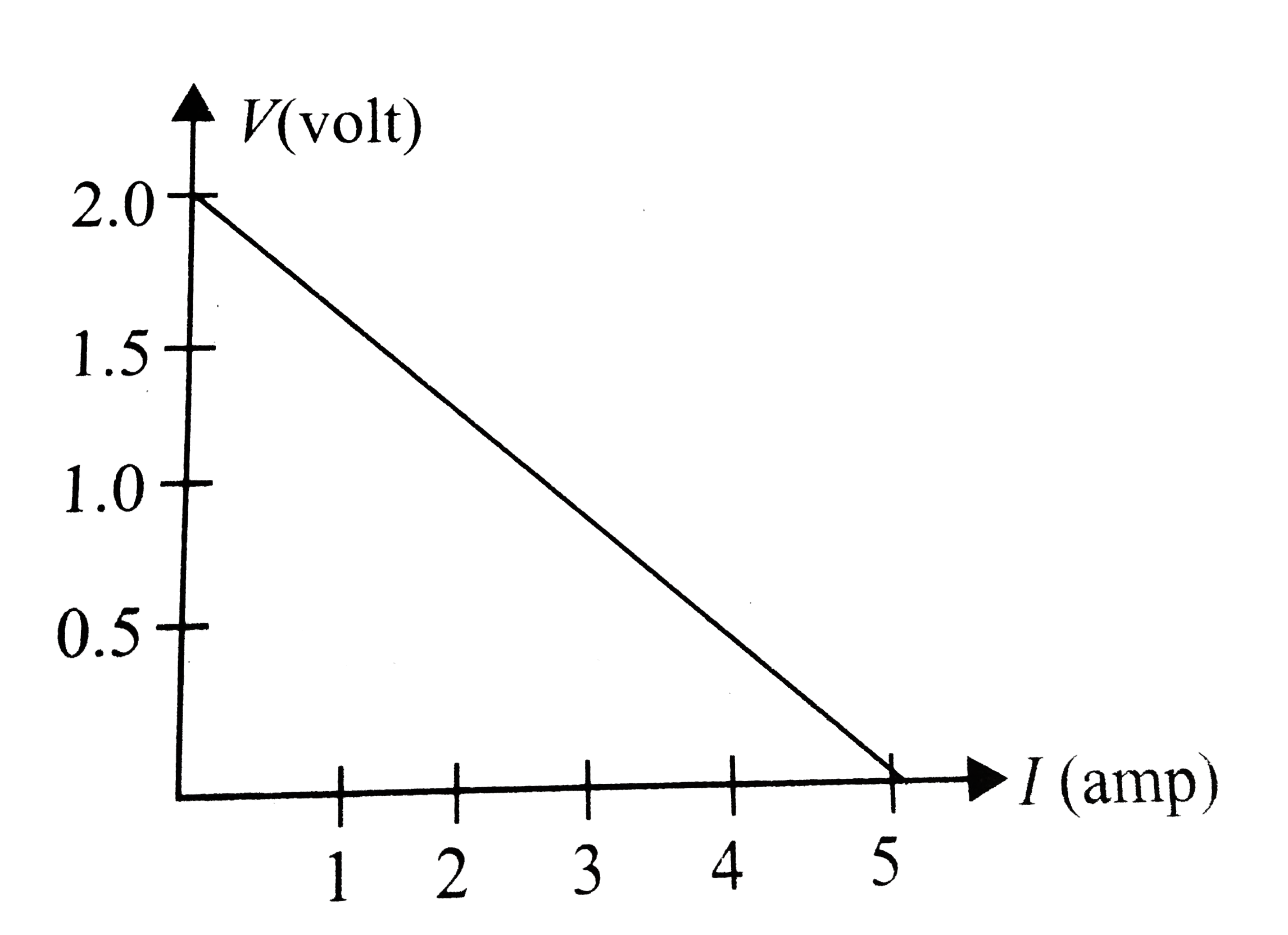
View SolutionA resistance R is connected across a cell of emf ε and internal resistance r. A potentiometer now measures the potential difference between the terminals of the cell is V. Write the expression for r in terms of ε, V and R.
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
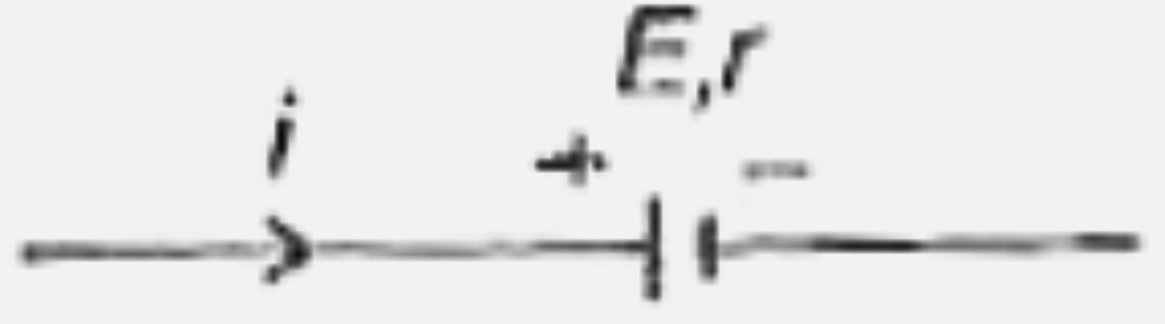
View SolutionThe emf of a cell is ε and its internal resistance is r. its terminals are connected to a resistance R. The potential difference between the terminals is 1.6V for R=4Ω, and 1.8V for R=9Ω. Then,
View SolutionWhat is the relationship between potential difference across the terminals of a cell and emf of the cell ?
View Solution