In the figure, the value of resistors to be connected between C and D so that the resistance of the entire circuit between A and B does not change with the number of elementary set used is
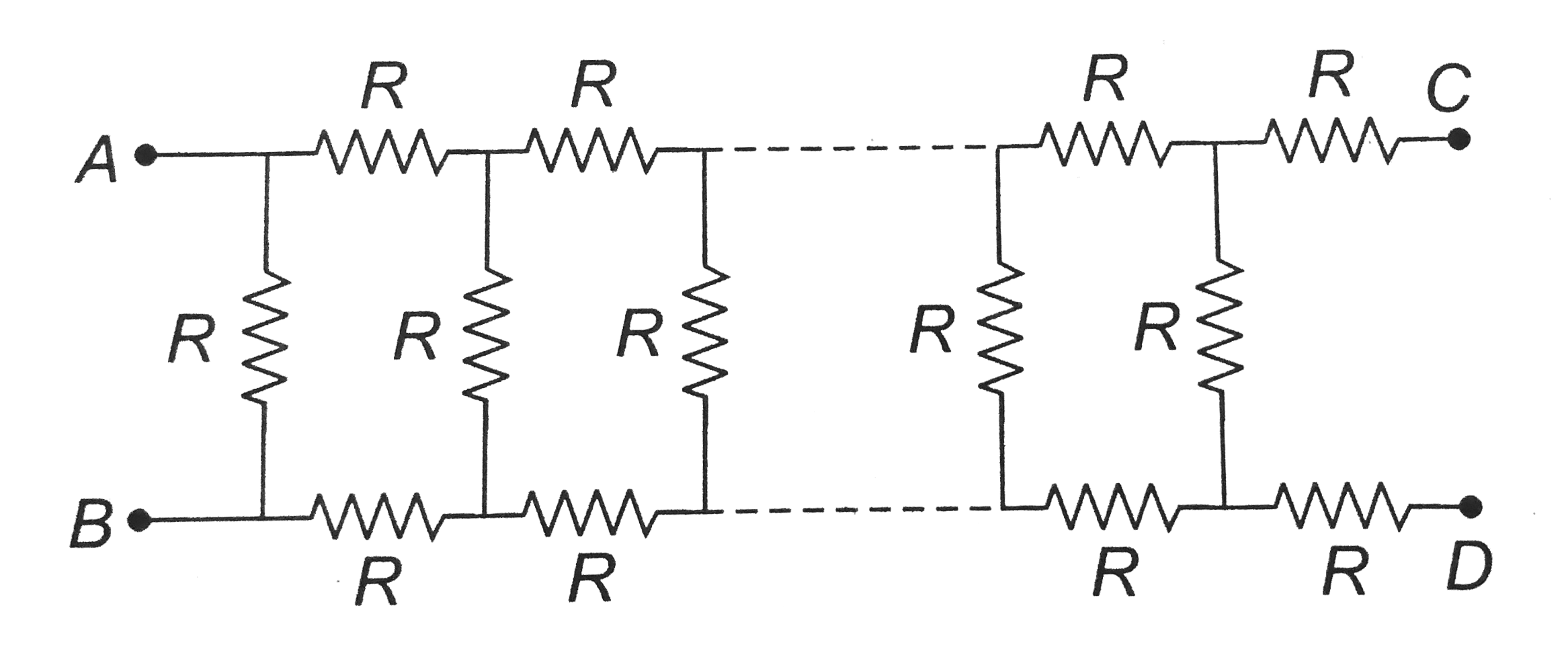
R
R(√3−1)
3R
R(√3−1)
The correct Answer is:B
Potential difference across C and D is 100 V
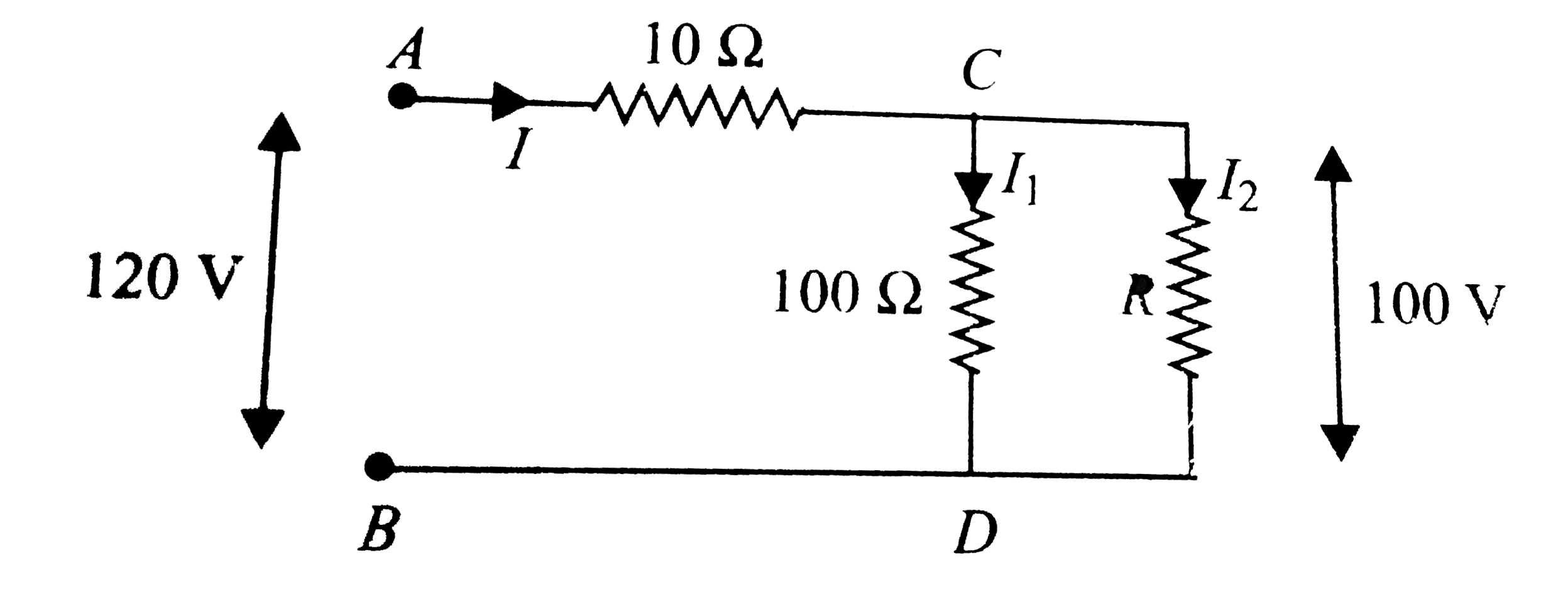
Hence I1=100100=1A,VAC=120−100=20KV
and I=20102A.Hence,I2=2−1=1A
R=100/I2=100Ω
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Comprehension
35 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
The resistance of the circuit between A and B is:-

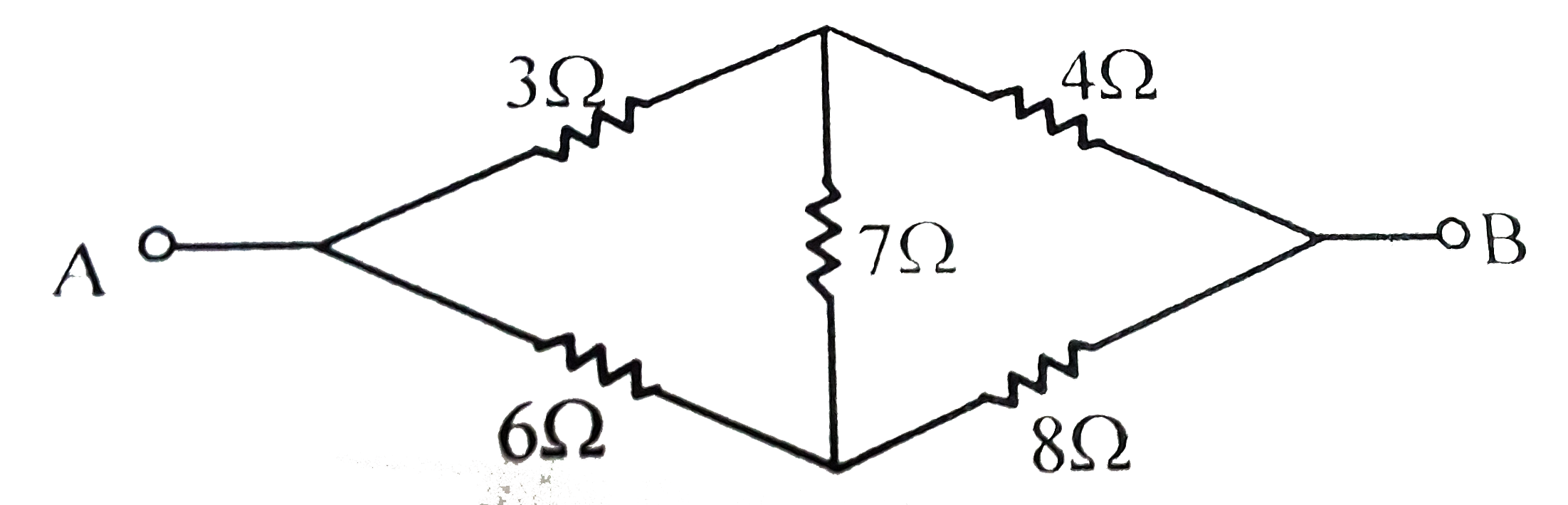
View SolutionCalculate the net resistance of the circuit between A and B:
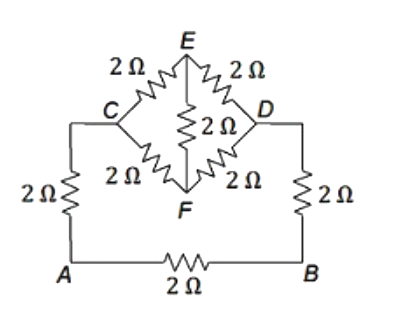
View SolutionThe resistance of the following circuit figure between A and B is
View SolutionIn the circuit shown here, what is the value of the unknown resistor R so that the total resistance of the circuit between points P and Q is also equal to R

View SolutionThe effective resistance between A and B is the given circuit is

View SolutionThree resistors are connected to a 6 V battery as shown in the figure
Calculate:
the equivalent resistance of the circuit
View SolutionThe effective resistance of the infinite resistance ladder circuit between terminais A and B as shown in the figure is
View SolutionFor the circuit shown in fig. the equivalent resistance between A and C is

View SolutionFind the net resistance between A and B in the circuit.
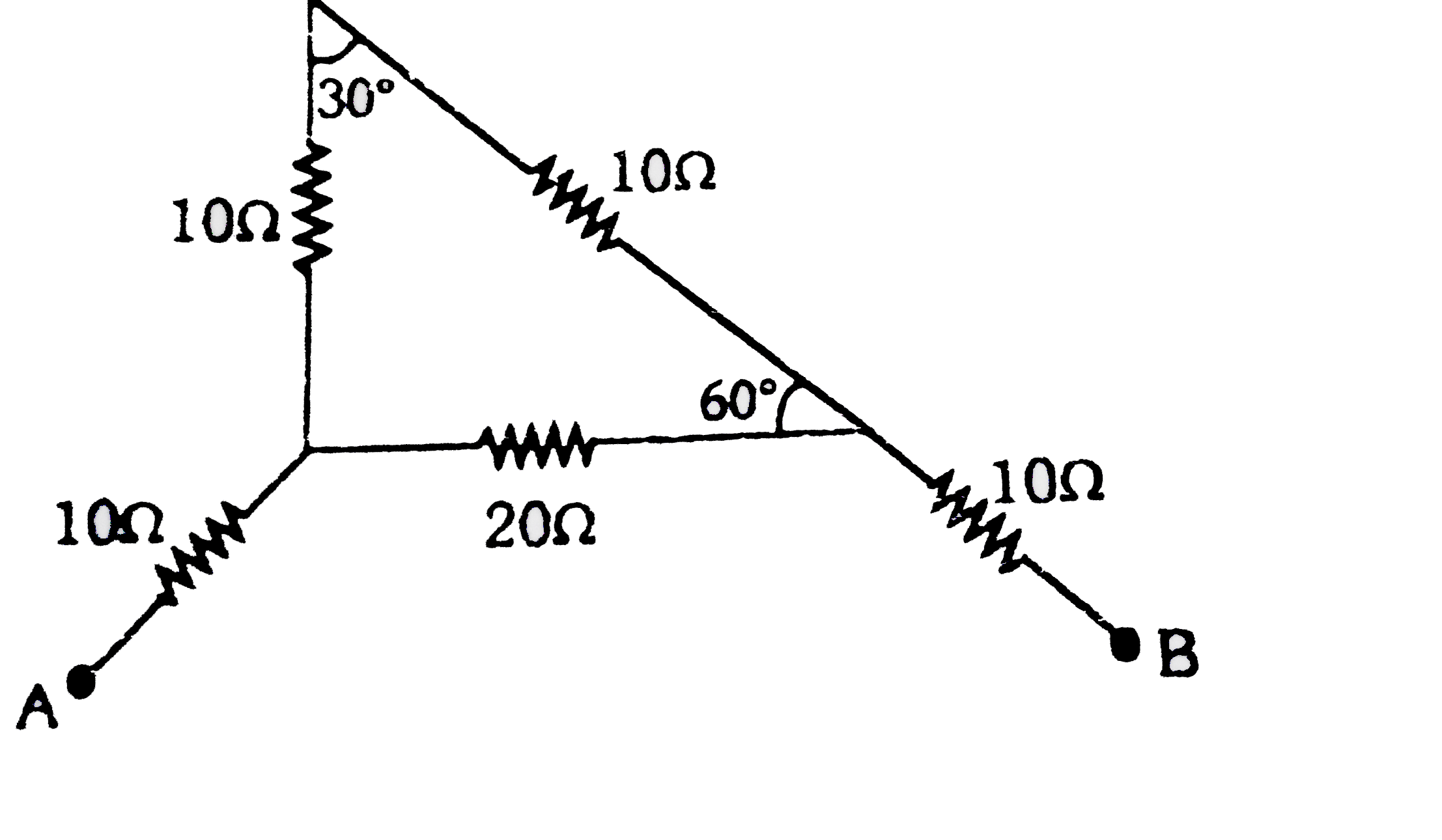
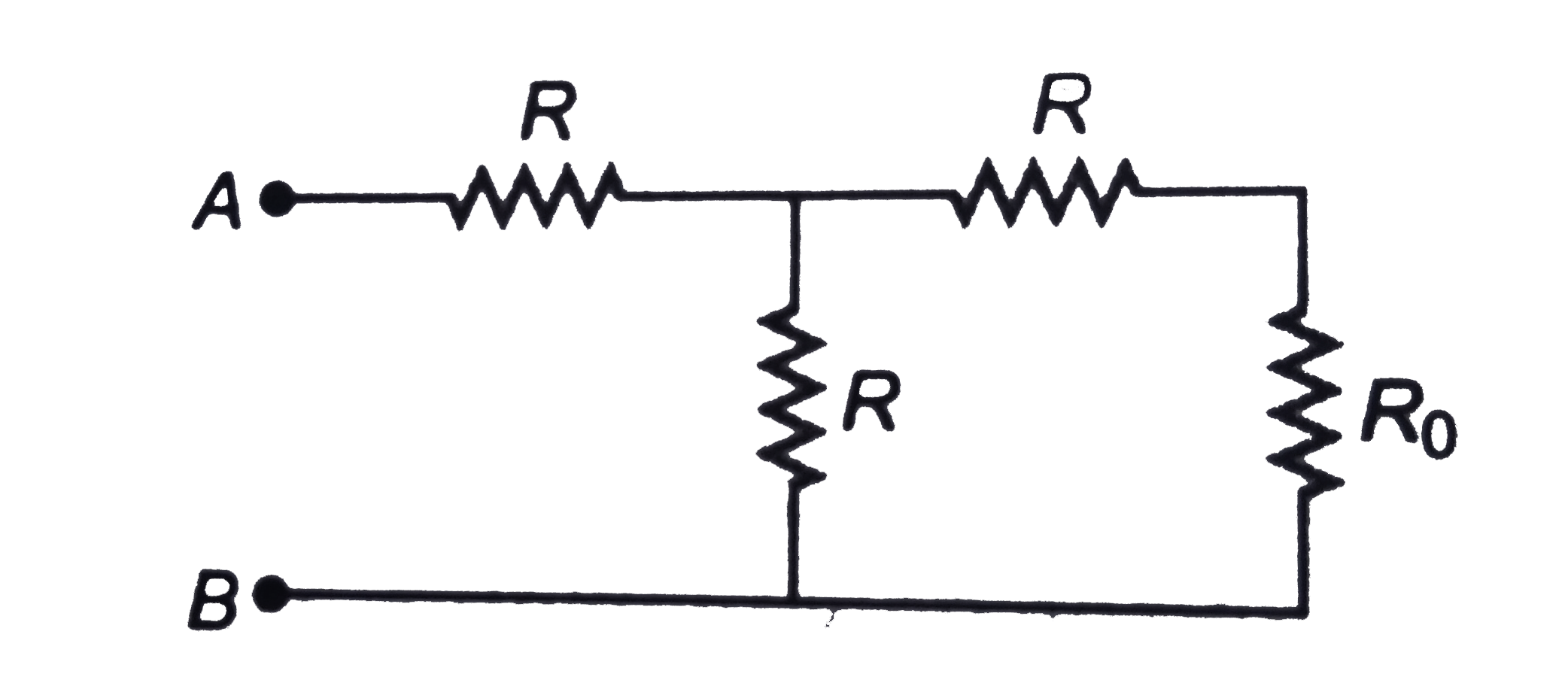
View SolutionIn the circuit shown in figure the total resistance between points A and B is R0. The value of resistance R is
View Solution
