A capacitor discharges through a resistance. The stored energy U0 in one capacitive time constant falls to
U0/e2
eU0
U0/e
none of the above
The correct Answer is:A
To solve the problem of how the stored energy in a capacitor discharging through a resistance falls to after one capacitive time constant, we can follow these steps:
1. Understand the Initial Energy Stored in the Capacitor:
The initial energy U0 stored in a capacitor with capacitance C and charge Q0 is given by the formula:
U0=Q202C
2. Determine the Charge After One Time Constant:
The charge Q on the capacitor at a time T is given by the equation:
Q=Q0e−T/τ
where τ=RC is the time constant of the circuit. For one time constant, T=τ:
Q=Q0e−1
Thus, at T=τ, the charge becomes:
Q=Q0e
3. Calculate the Energy Stored After One Time Constant:
The energy U stored in the capacitor after one time constant can be calculated using the new charge Q:
U=Q22C
Substituting Q=Q0e:
U=(Q0e)22C=Q202e2C
4. Relate the New Energy to the Initial Energy:
We can express the new energy U in terms of the initial energy U0:
U=1e2⋅Q202C=U0e2
5. Conclusion:
Therefore, after one capacitive time constant, the stored energy in the capacitor falls to:
U=U0e2
The initial energy U0 stored in a capacitor with capacitance C and charge Q0 is given by the formula:
U0=Q202C
The charge Q on the capacitor at a time T is given by the equation:
Q=Q0e−T/τ
where τ=RC is the time constant of the circuit. For one time constant, T=τ:
Q=Q0e−1
Thus, at T=τ, the charge becomes:
Q=Q0e
The energy U stored in the capacitor after one time constant can be calculated using the new charge Q:
U=Q22C
Substituting Q=Q0e:
U=(Q0e)22C=Q202e2C
We can express the new energy U in terms of the initial energy U0:
U=1e2⋅Q202C=U0e2
Therefore, after one capacitive time constant, the stored energy in the capacitor falls to:
U=U0e2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct16videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Comprehension35videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective29videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
A charged capacitor is discharged through a resistance. The time constant of the circuit is η. Then the value of time constant for the power dissipated through the resistance will be
View SolutionA capacitor of capacitance C is allowed to discharge through a resistance R. The net charge flown through resistance during one time constant is (I0 is the maximum current)
View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
View SolutionA capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
View SolutionA capacitor of capacitance 5μF is charged to a potential difference 200 V and then allowed to dischage through a resistance 1kΩ. The cahrge on the capacitor at the instant the current through the resistance is 100 Ma, is (in μC):
View SolutionA capacitance C charged to a potential difference V is discharged by connecting its plates through a resistance R. Find the heat dissipated in one time constant after the connections are made. Do this by calculating ∫i2Rdtand also by finding the decrease in the energy stored in the capacitor.
View SolutionFor the circuit shown in figure, find
(a) the initial current through each resistor
(b) steady state current through each resistor
(c) final energy stored in the capacitor
(d) time constant of the circuit when switch is opened.
 View Solution
View SolutionThe energy stored in the capacitor in the steady state is
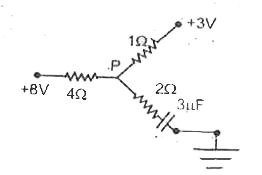 View Solution
View SolutionA charged capacitor of capacitance C is discharged through a resistance R. A radioactive sample decays with an average-life τ.Find the value of R for which the ratio of the electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant in time.
View SolutionLet C be the capacitance of a capacitor discharging through a resistor R. Suppose t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value and t2 is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio t1/t2 will be
View Solution
