A straight conductor of uniform cross section carries a time varying current, which varies at the rate dI//dt = I. If s is the specific charge that is carried by each charge carries of the conductor and l is the length of the condcutor, then the totalt force experienced by all the charge carries per unit length of the conductor due to their drift velocities only is
F=Is
F=I2√ls
F=Is
F=2Ils
The correct Answer is:C
To solve the problem, we need to determine the total force experienced by all the charge carriers per unit length of a straight conductor carrying a time-varying current. Here’s the step-by-step solution:
Step 1: Define the parameters
Let:
- I = current flowing through the conductor
- dIdt=I = rate of change of current
- s = specific charge carried by each charge carrier
- l = length of the conductor
- n = number of charge carriers per unit volume
- A = cross-sectional area of the conductor
- e = charge of an individual charge carrier (electron)
Step 2: Calculate the number of charge carriers in the conductor
The total volume of the conductor is given by A×l. Therefore, the total number of charge carriers in the conductor is:
N=n⋅A⋅l
Step 3: Calculate the drift velocity
The current I can be expressed in terms of the drift velocity vd:
I=n⋅A⋅e⋅vd
From this, we can solve for the drift velocity vd:
vd=In⋅A⋅e
Step 4: Calculate the momentum of charge carriers
The momentum P of all the charge carriers can be expressed as:
P=N⋅m⋅vd=(n⋅A⋅l)⋅m⋅vd
Substituting the expression for vd:
P=(n⋅A⋅l)⋅m⋅(In⋅A⋅e)
This simplifies to:
P=l⋅m⋅Ie
Step 5: Calculate the force using Newton's second law
According to Newton's second law, the force F is the rate of change of momentum:
F=dPdt
Substituting the expression for P:
F=ddt(l⋅m⋅Ie)=l⋅me⋅dIdt
Step 6: Relate dIdt to s
Given that dIdt=I and s=em (specific charge), we can express the force per unit length:
Fl=l⋅me⋅dIdt=l⋅me⋅I
Rearranging gives:
Fl=Is
Final Answer
Thus, the total force experienced by all the charge carriers per unit length of the conductor is:
Fl=Is
Let:
- I = current flowing through the conductor
- dIdt=I = rate of change of current
- s = specific charge carried by each charge carrier
- l = length of the conductor
- n = number of charge carriers per unit volume
- A = cross-sectional area of the conductor
- e = charge of an individual charge carrier (electron)
The total volume of the conductor is given by A×l. Therefore, the total number of charge carriers in the conductor is:
N=n⋅A⋅l
The current I can be expressed in terms of the drift velocity vd:
I=n⋅A⋅e⋅vd
From this, we can solve for the drift velocity vd:
vd=In⋅A⋅e
The momentum P of all the charge carriers can be expressed as:
P=N⋅m⋅vd=(n⋅A⋅l)⋅m⋅vd
Substituting the expression for vd:
P=(n⋅A⋅l)⋅m⋅(In⋅A⋅e)
This simplifies to:
P=l⋅m⋅Ie
According to Newton's second law, the force F is the rate of change of momentum:
F=dPdt
Substituting the expression for P:
F=ddt(l⋅m⋅Ie)=l⋅me⋅dIdt
Given that dIdt=I and s=em (specific charge), we can express the force per unit length:
Fl=l⋅me⋅dIdt=l⋅me⋅I
Rearranging gives:
Fl=Is
Thus, the total force experienced by all the charge carriers per unit length of the conductor is:
Fl=Is
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct
16 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Comprehension
35 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
The charge q flowing in a conductor of uniform cross section, varies with time as q=αt−bt2. Then, the current
View SolutionWhen a current carrying conductor is placed in a magnetic field, it experiences a mechanical force. What should be the angle between the magnetic field and the length of the conductor so that the force experienced is :
(i) Zero
(ii) Maximum ?
View SolutionA copper rod of cross sectional area A carries a uniform current I through it. At temperature T if the volume charge density of the rod is ρ how long will the charges take to travel a distance d?
View SolutionA condutor carrying current I is placed parallel to a current per unit width j0 and width d, as shown in the Find the force per unit length on the conductor
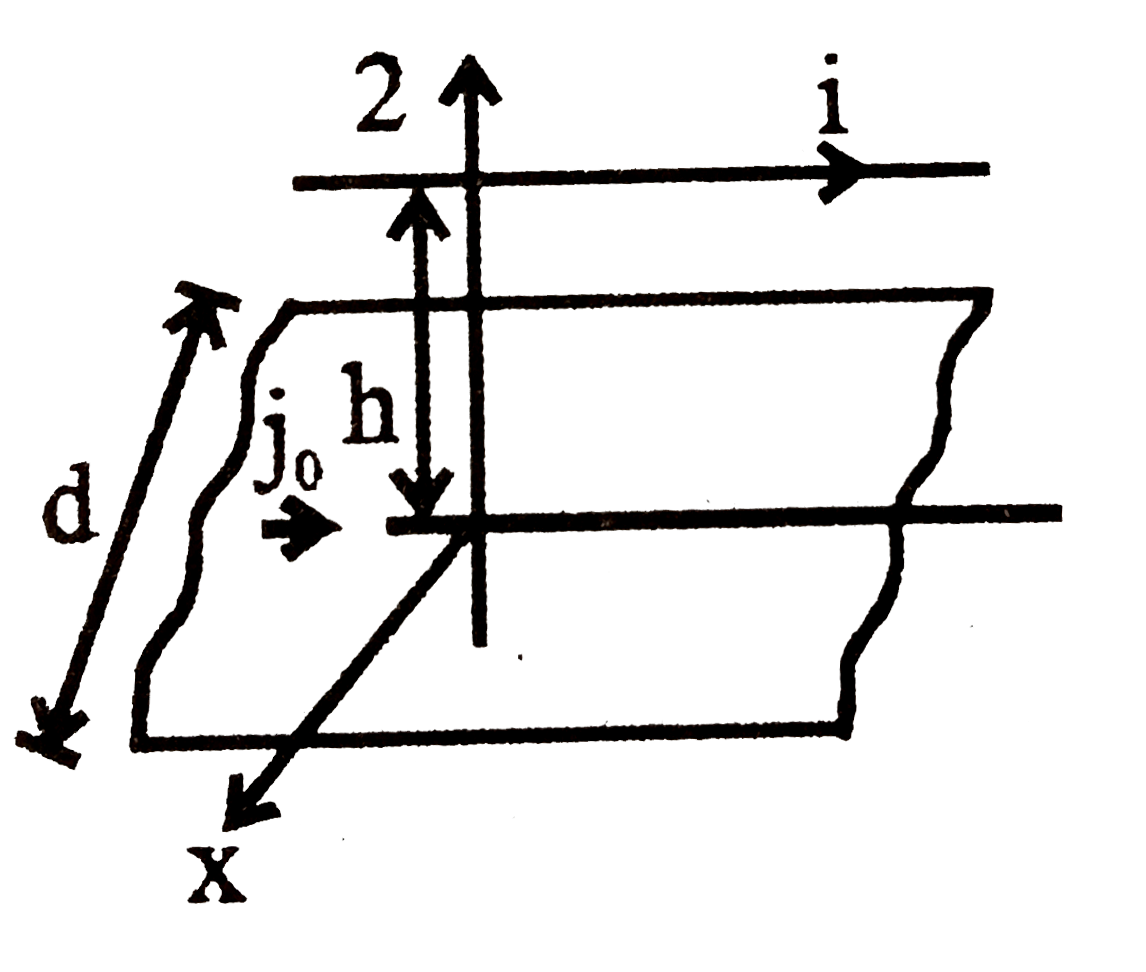 .
.
View SolutionA long, thick straight conductor of radius R carries current I uniformly distributed in its cross section area.The ratio of energy density of the magnetic field at distance R/2 from surface inside the conductor and outside the conductor is:
View SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View SolutionDefine the term mobility of charge carriers in a current carrying conductor. Obtain the relation for mobility in terms of relaxation time.
View SolutionLong, straight conductors with square cross sections and each carrying current I are laid side-by-side to form an infinite current sheet as shown in Fig. The conductor lies in the x-y plane, are parallel to the y-axis and carry current in the +y direction. There are n conductors per unit length measured along x-axis.

what are the magnitude and direction of the magnetic field for distance a below the current sheet?
View SolutionThe current in a conductor varies with time .t. as I=3t+4t2. Where I in amp and t in sec. The electric charge flows through the section of the conductor between t = 1s and t = 3s
View Solution
