A capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
changes with time
does not change with time and it is equal to time constant of circuit
does not change with time, but not equal to time constant of circuit
may or may not change depending upon the charge given to the capacitor
The correct Answer is:B
To solve the problem regarding the ratio of charge on a capacitor to the current in the circuit during the discharge process, we can follow these steps:
Step 1: Understand the Discharge Equation of a Capacitor
When a capacitor discharges through a resistor, the charge Q on the capacitor at any time t is given by the equation:
Q(t)=Q0e−tRC
where:
- Q0 is the initial charge on the capacitor,
- R is the resistance,
- C is the capacitance,
- t is the time,
- e is the base of the natural logarithm.
Step 2: Find the Current in the Circuit
The current I in the circuit can be found by differentiating the charge with respect to time:
I(t)=−dQdt=−ddt(Q0e−tRC)
Using the chain rule, we get:
I(t)=Q0RCe−tRC
Step 3: Calculate the Ratio of Charge to Current
Now, we need to find the ratio of charge Q to current I:
QI=Q0e−tRCQ0RCe−tRC
Here, the Q0e−tRC terms cancel out:
QI=RC
Step 4: Analyze the Result
The ratio QI=RC shows that:
- The ratio of charge on the capacitor to the current in the circuit is equal to the time constant τ=RC.
- This ratio does not change with time since R and C are constants.
Conclusion
Thus, the ratio of charge on the capacitor to the current in the circuit is equal to the time constant RC and does not change with time.
Final Answer
The ratio of charge on the capacitor to the current in the circuit is RC, which is constant and equal to the time constant.
---
When a capacitor discharges through a resistor, the charge Q on the capacitor at any time t is given by the equation:
Q(t)=Q0e−tRC
where:
- Q0 is the initial charge on the capacitor,
- R is the resistance,
- C is the capacitance,
- t is the time,
- e is the base of the natural logarithm.
The current I in the circuit can be found by differentiating the charge with respect to time:
I(t)=−dQdt=−ddt(Q0e−tRC)
Using the chain rule, we get:
I(t)=Q0RCe−tRC
Now, we need to find the ratio of charge Q to current I:
QI=Q0e−tRCQ0RCe−tRC
Here, the Q0e−tRC terms cancel out:
QI=RC
The ratio QI=RC shows that:
- The ratio of charge on the capacitor to the current in the circuit is equal to the time constant τ=RC.
- This ratio does not change with time since R and C are constants.
Thus, the ratio of charge on the capacitor to the current in the circuit is equal to the time constant RC and does not change with time.
The ratio of charge on the capacitor to the current in the circuit is RC, which is constant and equal to the time constant.
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Multiple Correct
Explore 16 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Comprehension
Explore 35 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Subjective
Explore 29 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
A capacitor of capacitance 5μF is charged to a potential difference 200 V and then allowed to dischage through a resistance 1kΩ. The cahrge on the capacitor at the instant the current through the resistance is 100 Ma, is (in μC):
View SolutionDetermine to charge on the capacitor in the following circuit :
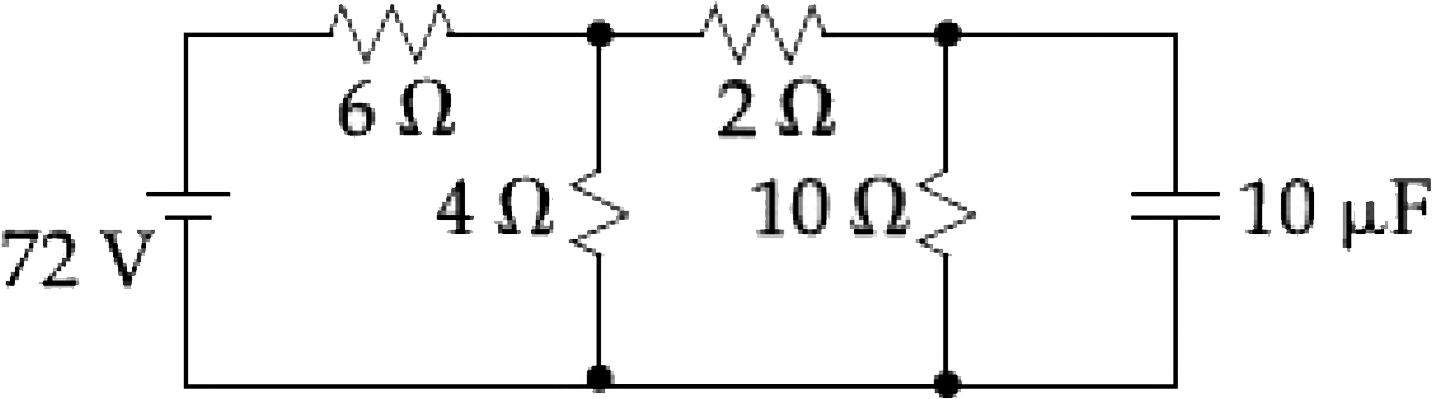
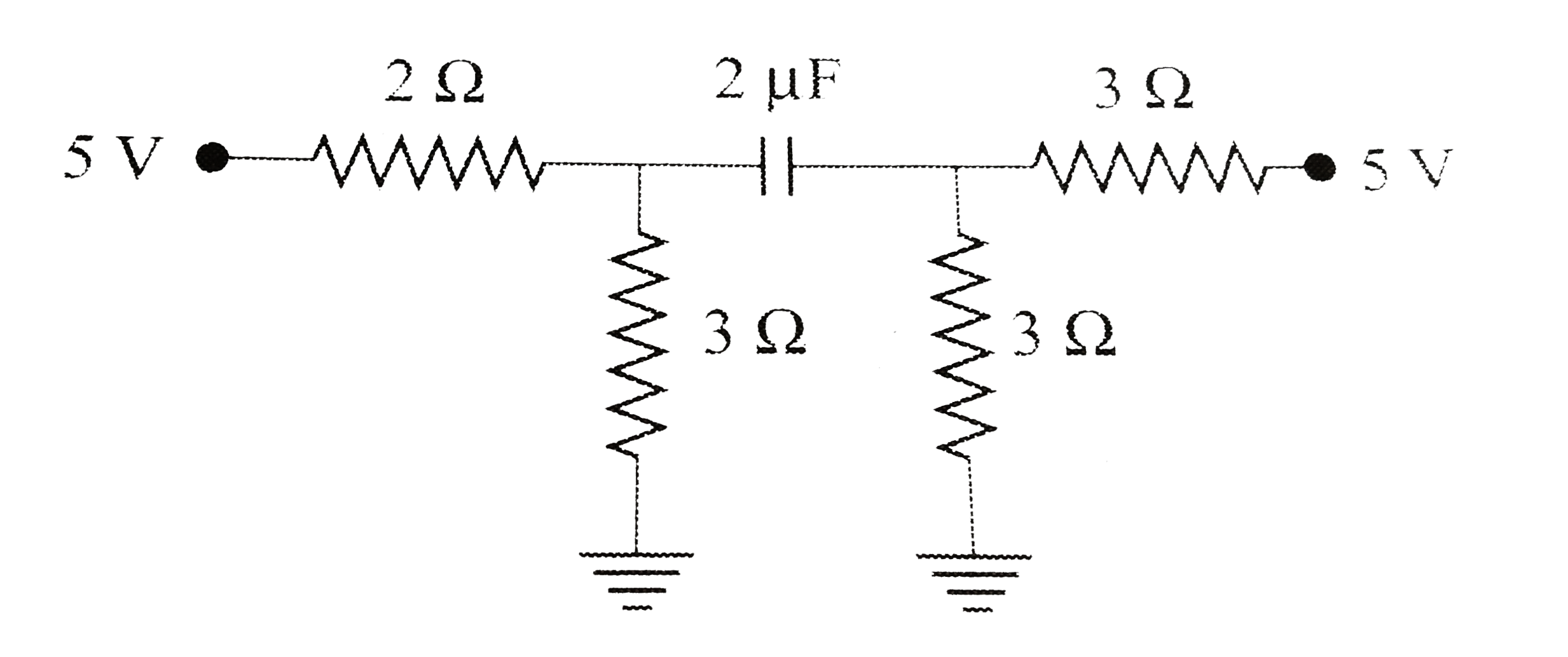
View SolutionThe charge on the capacitor in steady state in the circuit shown is
View SolutionWhen a capacitor discharges through a resistance R, the time constant is τ and the maximum current in the circuit is i0. Then,
View SolutionA capacitor of capacitance C is allowed to discharge through a resistance R. The net charge flown through resistance during one time constant is (I0 is the maximum current)
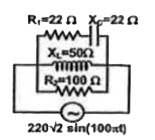
View SolutionThe current through the capacitor in the given circuit is
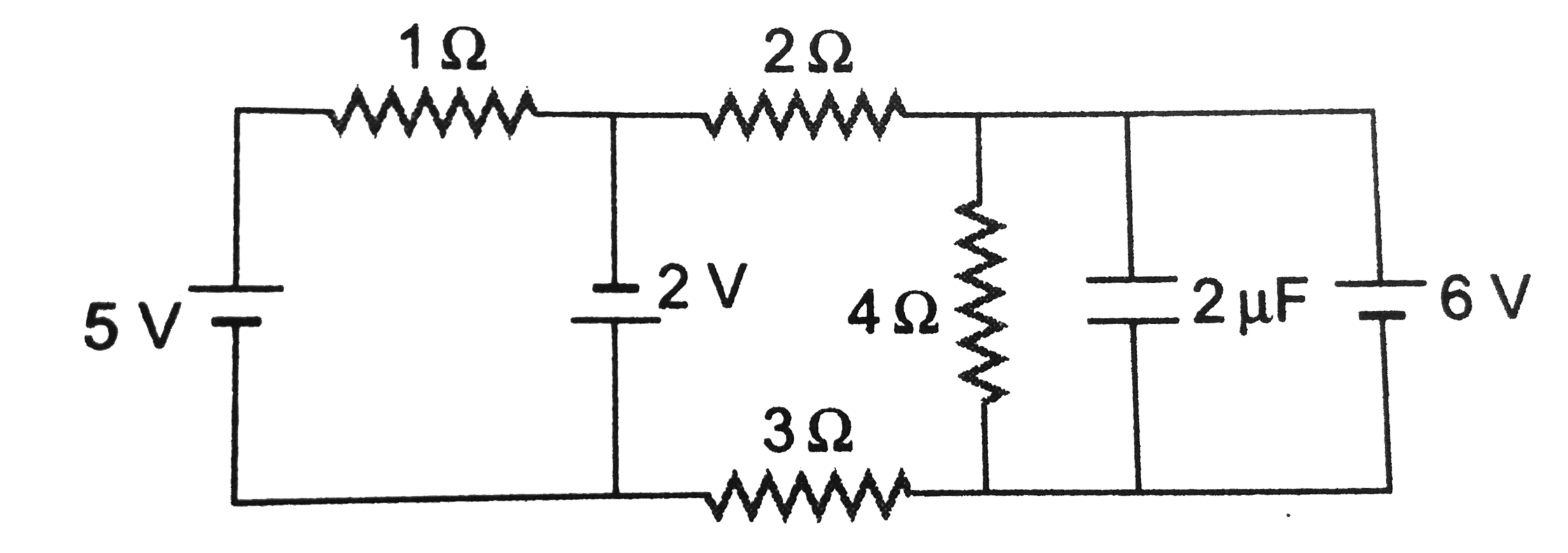
View SolutionThe current in 1Ω resistance and charge stored in the capacitor are
View SolutionA radioactive sample decays with an average life of 20ms. A capacitor of capacitance 100μF is charged to some potential and then the plates are connected through a resistance R. What should be the value of R so that the ratio of the charge on the capacitor to the activity of the radioactive sample remains constant in time?
View SolutionThe charge deposited on 4μF capacitor in the given circuit is:
View SolutionTwo identical capacitors A and B are charged to the same potential and then made to discharge through resistances RA and RB respectively, with RA>RB.
View Solution