A capacitor of capacitance 5μF is charged to a potential difference 200 V and then allowed to dischage through a resistance 1kΩ. The cahrge on the capacitor at the instant the current through the resistance is 100 Ma, is (in μC):
(a)50
(b)100
(c)500
(d)1000
The correct Answer is:C
To solve the problem step by step, we will follow the principles of capacitors and Ohm's law.
Step 1: Understand the given values
- Capacitance C=5μF=5×10−6F
- Initial potential difference V0=200V
- Resistance R=1kΩ=1000Ω
- Current I=100mA=0.1A
Step 2: Calculate the potential difference across the capacitor when the current is 100 mA
Using Ohm's law, we know that:
V=I×R
Substituting the values:
V=0.1A×1000Ω=100V
Step 3: Relate the charge on the capacitor to the potential difference
The charge Q on the capacitor is given by the formula:
Q=C×V
Substituting the values we have:
Q=5×10−6F×100V
Step 4: Calculate the charge
Calculating the above expression:
Q=5×10−6×100=5×10−4C
Step 5: Convert the charge into microcoulombs
To convert coulombs to microcoulombs:
Q=5×10−4C=500μC
Final Answer
The charge on the capacitor at the instant the current through the resistance is 100 mA is 500 µC.
---
- Capacitance C=5μF=5×10−6F
- Initial potential difference V0=200V
- Resistance R=1kΩ=1000Ω
- Current I=100mA=0.1A
Using Ohm's law, we know that:
V=I×R
Substituting the values:
V=0.1A×1000Ω=100V
The charge Q on the capacitor is given by the formula:
Q=C×V
Substituting the values we have:
Q=5×10−6F×100V
Calculating the above expression:
Q=5×10−6×100=5×10−4C
To convert coulombs to microcoulombs:
Q=5×10−4C=500μC
The charge on the capacitor at the instant the current through the resistance is 100 mA is 500 µC.
Topper's Solved these Questions
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:LEVEL 2
Explore 40 Videos
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Main (Archive) LEVEL-1
Explore 36 Videos
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:LEVEL 0 (LONG ANSWER TYPE)
Explore 3 Videos
- BASIC MATHEMATICS & VECTORSBook:VMC MODULES ENGLISHChapter:BASIC MATHEMATICS & VECTORSExercise:Impeccable
Explore 50 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
Similar Questions
A capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
View SolutionA capacitor of capacitance 5μF is charged to a potential difference 100V and then diconnected from the powerr supply. The minimum work needed to pull the plates of the capacitor apart so that the distance between them doubles is (in mJ).
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
View SolutionA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
View SolutionThe current in 1Ω resistance and charge stored in the capacitor are
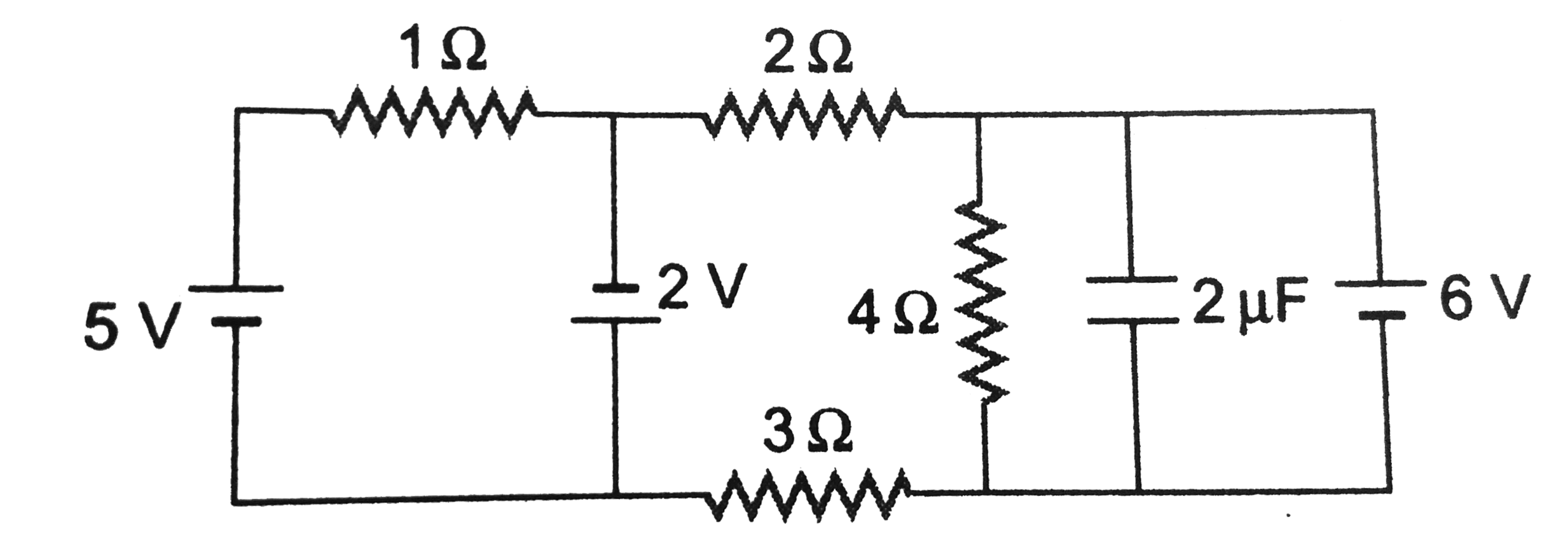
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
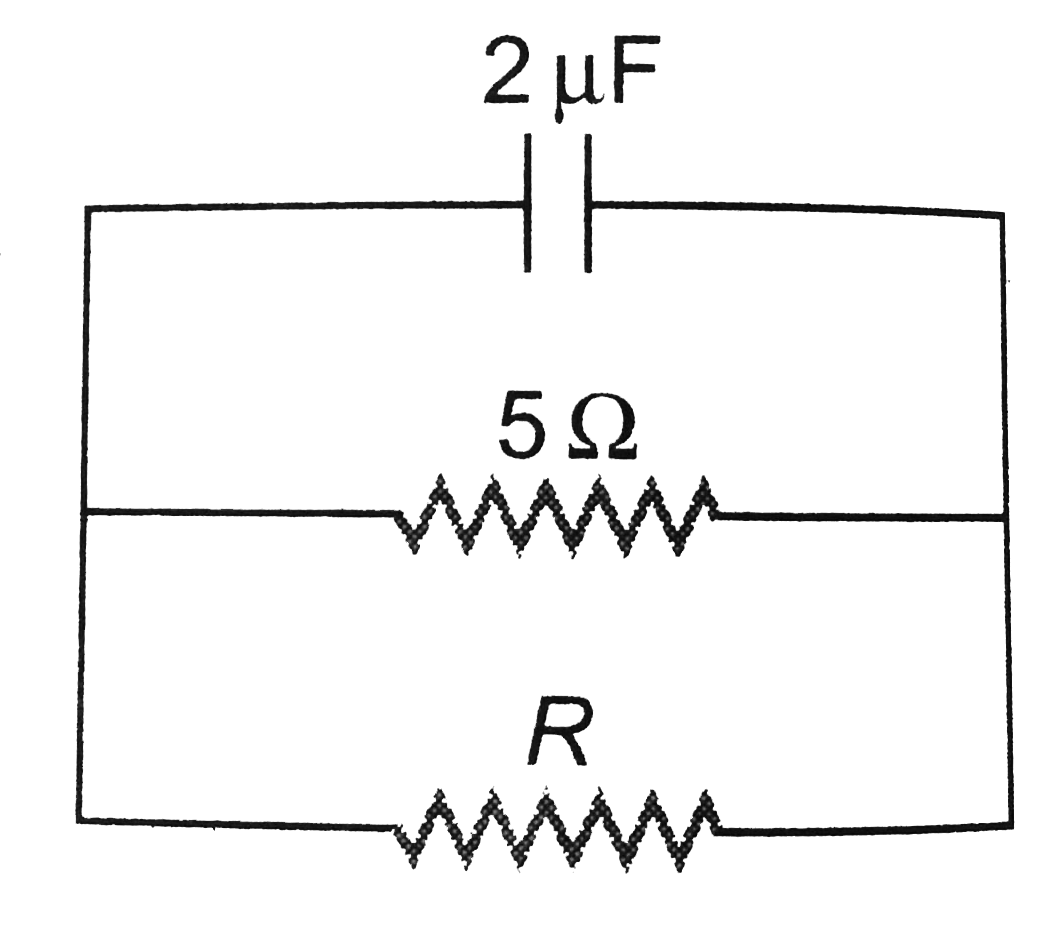
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to

View SolutionA capacitor of capacitance C is charged to a potential difference V0 and then connected with a resistance and a battery of EMF 3V0 such that the positively charged plate of the capacitor is connected to the positive terminal of the battery. The total heat generated in the resistance until the current in the circuit becomes zero is n(CV20). the value of n is ________.
View Solution