Two capacitances of capacity C1and C2 are connected in series and potential difference V is applied across it. Then the potential difference across C1 will be
V2
(C22C21+C22)V
(C1C1+C2)V
(C2C1+C2)V
The correct Answer is:D
To find the potential difference across capacitor C1 when two capacitors C1 and C2 are connected in series and a potential difference V is applied across them, we can follow these steps:
1. Understanding Series Connection:
In a series connection of capacitors, the charge Q on each capacitor is the same. The total potential difference V across the series combination is the sum of the potential differences across each capacitor.
2. Charge Relationship:
Since both capacitors have the same charge Q, we can express the charge on each capacitor:
Q=C1V1=C2V2
where V1 is the potential difference across C1 and V2 is the potential difference across C2.
3. Total Voltage:
The total voltage across the series combination is given by:
V=V1+V2
4. Expressing V2:
From the charge relationship, we can express V2 in terms of Q:
V2=QC2
5. Substituting V2:
Substitute V2 into the total voltage equation:
V=V1+QC2
6. Expressing V1:
From the charge relationship, we can also express Q in terms of V1:
Q=C1V1
Substitute this into the equation for V:
V=V1+C1V1C2
7. Factoring Out V1:
Factor V1 out from the right-hand side:
V=V1(1+C1C2)
8. Solving for V1:
Now, solve for V1:
V1=V1+C1C2=VC2C1+C2
9. Final Expression:
Therefore, the potential difference across capacitor C1 is:
V1=C2C1+C2V
Final Answer:
The potential difference across capacitor C1 is given by:
V1=C2C1+C2V
In a series connection of capacitors, the charge Q on each capacitor is the same. The total potential difference V across the series combination is the sum of the potential differences across each capacitor.
Since both capacitors have the same charge Q, we can express the charge on each capacitor:
Q=C1V1=C2V2
where V1 is the potential difference across C1 and V2 is the potential difference across C2.
The total voltage across the series combination is given by:
V=V1+V2
From the charge relationship, we can express V2 in terms of Q:
V2=QC2
Substitute V2 into the total voltage equation:
V=V1+QC2
From the charge relationship, we can also express Q in terms of V1:
Q=C1V1
Substitute this into the equation for V:
V=V1+C1V1C2
Factor V1 out from the right-hand side:
V=V1(1+C1C2)
Now, solve for V1:
V1=V1+C1C2=VC2C1+C2
Therefore, the potential difference across capacitor C1 is:
V1=C2C1+C2V
The potential difference across capacitor C1 is given by:
V1=C2C1+C2V
Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - LEVEL 2
40 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Main (Archive) LEVEL-1
36 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - LEVEL 0 (LONG ANSWER TYPE)
3 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
Find the potential difference across C2.
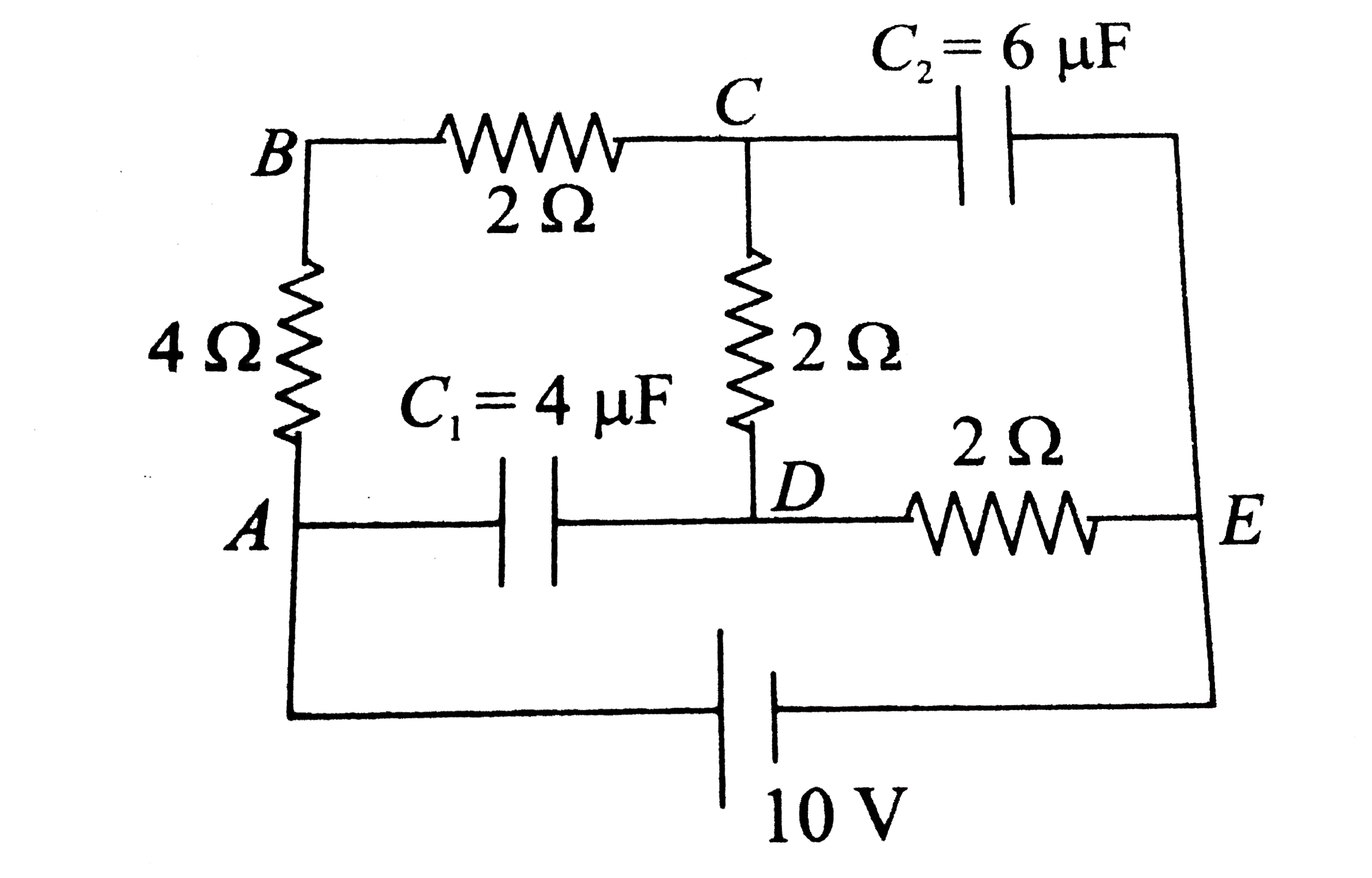
View SolutionWhen a potential difference is applied across, the current passing through
View SolutionTwo capacitors with capacitances C1andC2 are connected in series. Find the resultant capacitance.
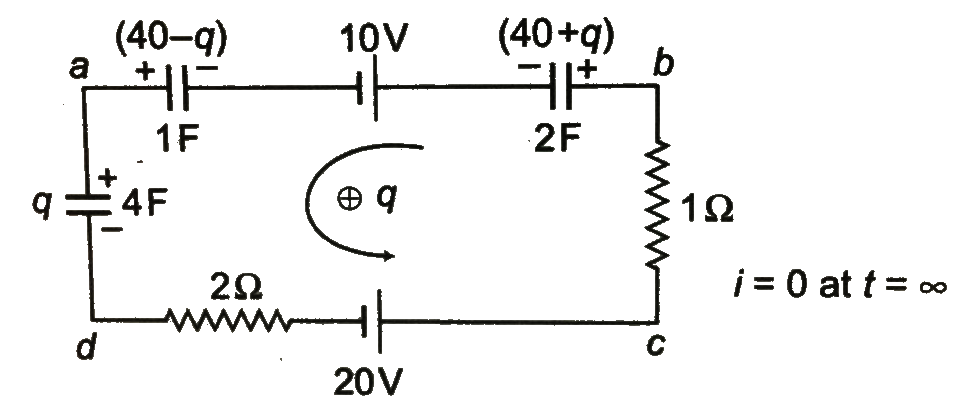
View SolutionIn the circuit shown as potential difference of 60V is appliled across AB. The potential difference between the points M and N is
View SolutionIn the figure the potential difference across 6 ohm resistor is 48 V. Then the potential difference between A and B is
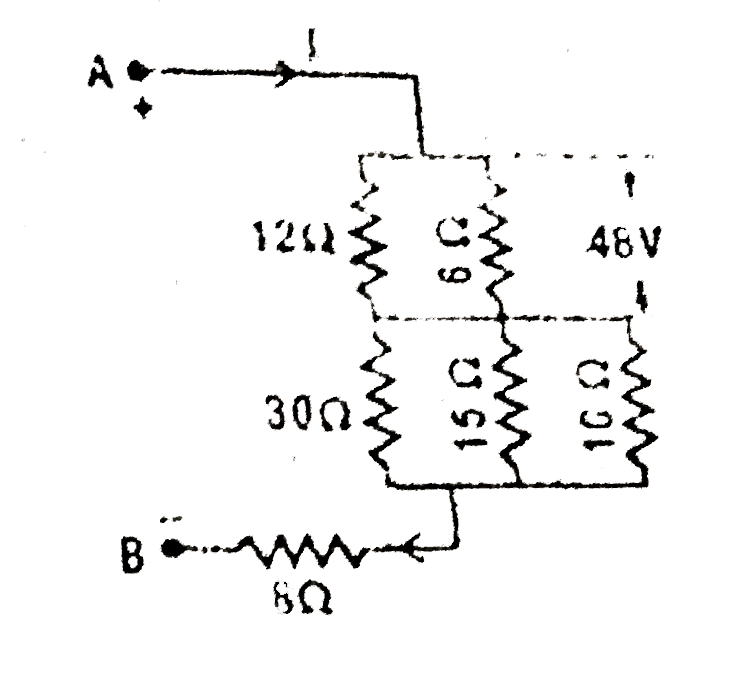
View SolutionIf the potential difference applied across a Coolidge tube is increased , then
View SolutionIf the potential difference applied across a Coolidge tube is increased , then
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the potential difference across the 6 Ω resistor.
View SolutionThree capacitors each of capacitance 9 pF are connected in series. What is the total capacitance of the combination ?
View Solution