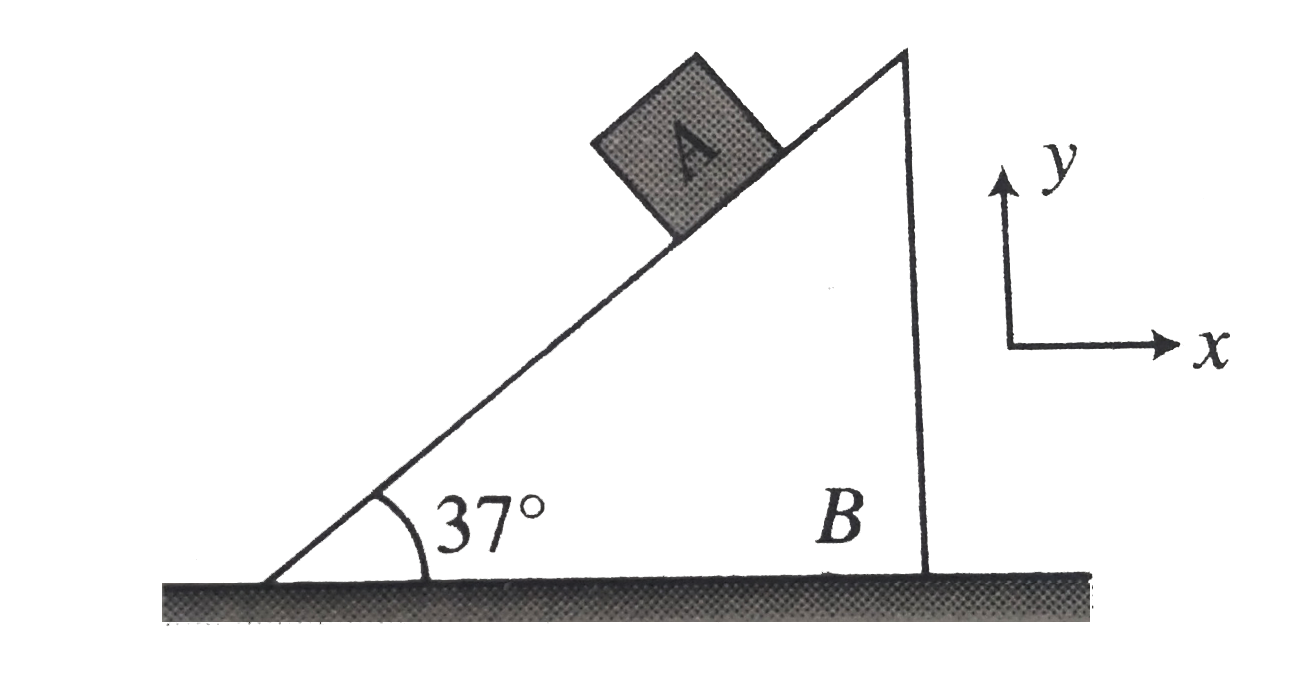
In fig, the acceleration of A is →aA=15ˆi+15ˆj. Then the acceleration of B is (A remains in constact with B)
6ˆi
−15ˆi
−10ˆi
−5ˆi
The correct Answer is:D

From wedge constant
(aA)⊥=(aB)⊥
aAXcos53∘−aAYcos37∘=aBcos53∘
aB=−5m/s⇒→aB=−5ˆi
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.39
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.40
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.37
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A charged particle moving in a magnetic field →B=ˆi−ˆj tesla, has an acceleration of 2ˆi+αˆj at some instant. Find the value of α
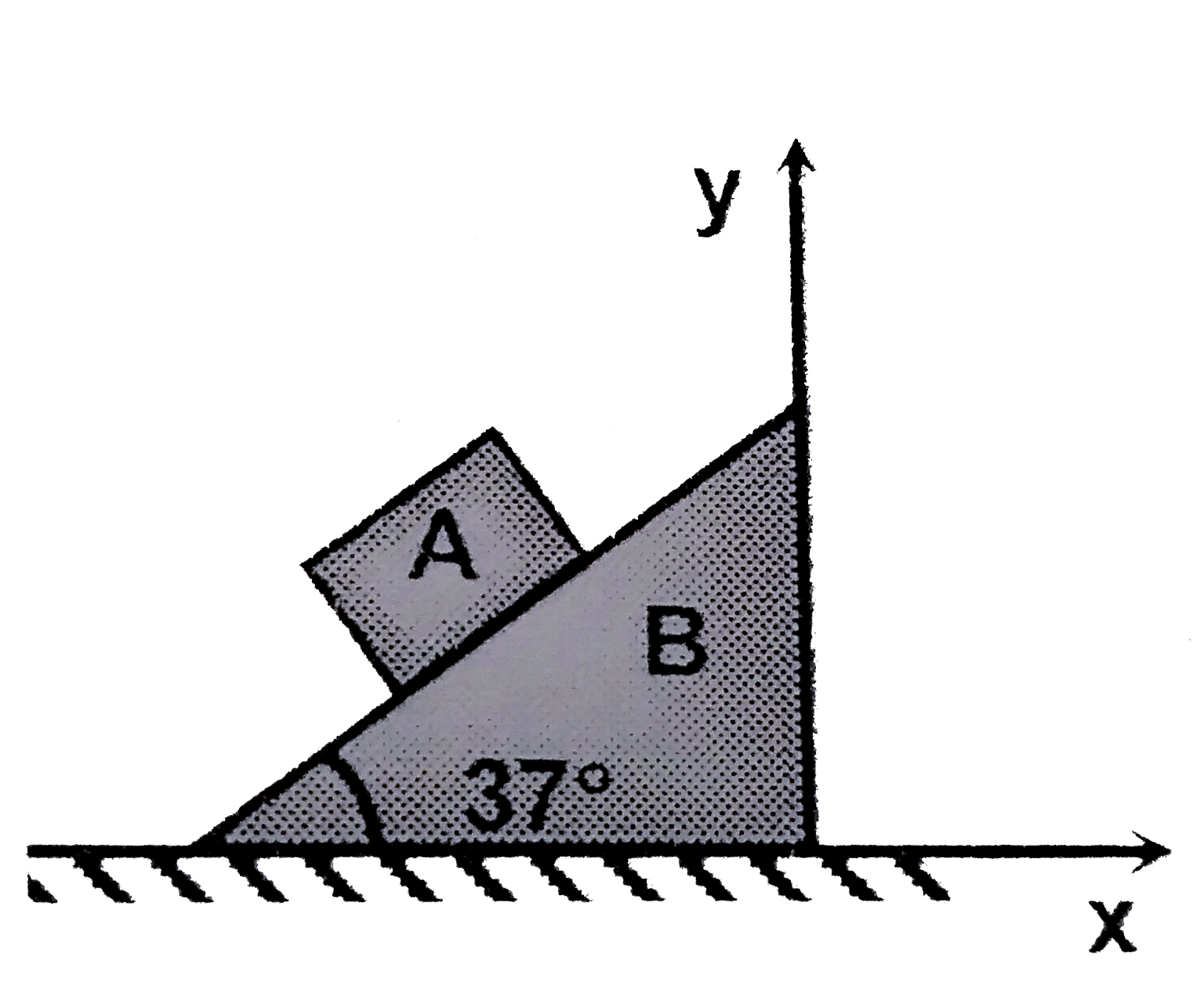
View SolutionIn the figure shown the velocity of A with respect to ground is (20ˆi+15ˆj)m/s, then what will be the magnitude of velocity of the wedge 'B' with respect to ground frame. (A remains in contact with B)
View Solution
Knowledge Check
If →a=2ˆi−ˆj+ˆkand→b=ˆi−2ˆj+ˆk then projection of →b'on'→a is
A5√63B5√6C5√6D5√6
The compenent of →A=ˆi+ˆj+5ˆk perpendicular to →B=3ˆi+4ˆj is
View SolutionA point charge +q0 is projected in a magnetic field →B=(ˆi+2ˆj−3ˆk). If acceleration of the particle is →a=(2ˆi+bˆj+ˆk) then value of b will be
View SolutionA charged particle has acceleration →a=2ˆi+xˆj in a megnetic field →B=−3ˆi+2ˆj−4ˆk. Find the value of x.
View SolutionFind the angle between →A=ˆi+2ˆj−ˆkand→B=−ˆi+ˆj−2ˆk
View SolutionWhich of the following is not true ? If →A=3ˆi+4ˆj and →B=6ˆi+8ˆj where A and B are the magnitude of →A and →B ?
View Solutionlet →a=2ˆi+3ˆj and →b=ˆi+4ˆj then find projection of →a on →b
View SolutionIf →A=−ˆi+3ˆj+2ˆkand→B=3ˆi+2ˆj+2ˆk then find the value of →A×→B.
View Solution
