The internal resistance of an accumulator battery of emf 6V is 10(Ω)when it is fully discharged,As the battery gets charged up.its internal resistance decreases to 1(Ω)The battery in its completely discharged state is connected to a charger which maintains a constant potential difference of 9 V.Find the current through the battery (a)just after the connections are made and (b) after a long time when it is completely charged.
To solve the problem step by step, we will analyze the situation of the battery being charged and calculate the current at two different instances: just after the connections are made and after a long time when the battery is fully charged.
Given Data:
- EMF of the battery (E) = 6 V
- Internal resistance when fully discharged (R1) = 10 Ω
- Internal resistance when fully charged (R2) = 1 Ω
- Potential difference maintained by the charger (V_ext) = 9 V
Step 1: Determine the net potential difference across the internal resistance when the battery is connected to the charger.
The net potential difference (V_net) across the internal resistance can be calculated as:
Vnet=Vext−E
Substituting the values:
Vnet=9V−6V=3V
Step 2: Calculate the current just after the connections are made (when the battery is fully discharged).
Using Ohm's law, the current (I) can be calculated using the formula:
I=VnetR1
Substituting the values:
I=3V10Ω=0.3A
Step 3: Calculate the current after a long time when the battery is completely charged.
When the battery is fully charged, the internal resistance changes to R2:
I=VnetR2
Substituting the new internal resistance value:
I=3V1Ω=3A
Final Answers:
(a) The current just after the connections are made is 0.3 A.
(b) The current after a long time when the battery is completely charged is 3 A.
---
- EMF of the battery (E) = 6 V
- Internal resistance when fully discharged (R1) = 10 Ω
- Internal resistance when fully charged (R2) = 1 Ω
- Potential difference maintained by the charger (V_ext) = 9 V
Vnet=Vext−E
Substituting the values:
Vnet=9V−6V=3V
I=VnetR1
Substituting the values:
I=3V10Ω=0.3A
I=VnetR2
Substituting the new internal resistance value:
I=3V1Ω=3A
(a) The current just after the connections are made is 0.3 A.
(b) The current after a long time when the battery is completely charged is 3 A.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
A battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current through the battery,
View SolutionA 20(μ)Fcapacitor is joined to a battery of emf 6.0V through a resistance of 100(Ω).find the charge on the capacitor 2.0ms after the connections are made .
View SolutionA coil having inductance 2.0 H and resistance 20Ω is connected to a battery of emf 4.0 V. Find (a) the current a the instant 0.20 s after the connection Is made and (b) the magnetic energy at this instant.
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionAn inductor coil of resistance 10Ω and inductance 120 mH is connected across a battery of emf 6 V and internal resistance 2Ω. Find the charge which flows through the inductor in (a) 10 ms, (b) 20ms and (c ) 100ms after the connections are made.
View SolutionThree identical cells each of emf 2 V and internal resistance 1Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6Ω Find the current delivered by the battery.
View SolutionTwo batteries of emf 4 V and 8 V with internal resistances 1Ω and 2Ω are connected in a circuit with a resistance of 9Ω as shown in figure. The current and potential difference between the points P and Q are
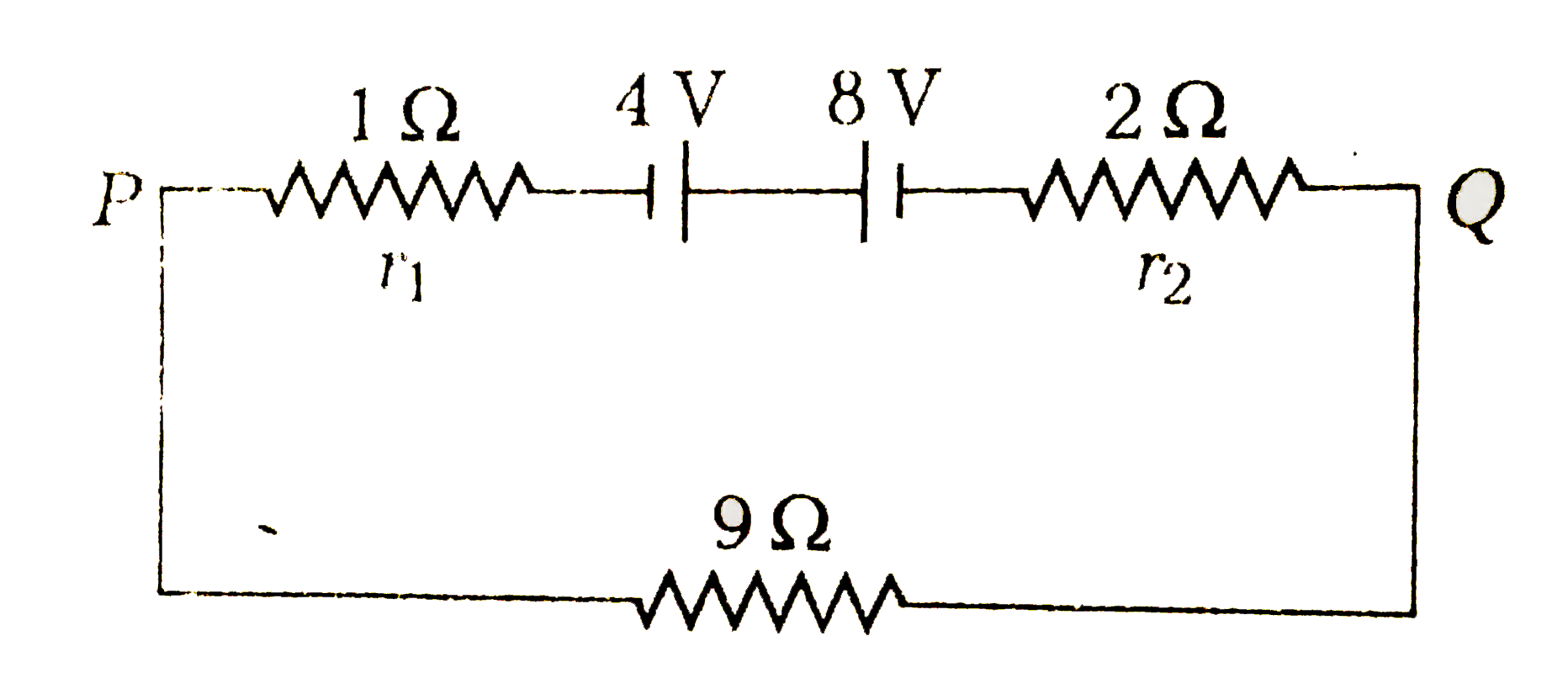
View SolutionA battery of emf 2.0V and internal resistance 0.10Ω is being charged with a current of 5.0A. Find the potential difference between the terminals of the battery?
View SolutionCalculate the current flowing through a wire of resistance 7.5 Ω connected to a battery of potential difference 1.5. V.
View SolutionCalculate the current flowing through a wire of resistance 5 Ω connected to a battery of potential difference 3 V.
View Solution
