Two identical parallel plate capacitors, of capacitance C each, have plates of area A, separated by a distance d. The space between the plates of the two capacitors, is filled with three dielectrics, of equal thickness and dielectric constants K1,K2andK3. The first capacitor is filled as shown in fig. I, and the second one is filled as shown in fig. II. If these two modified capacitors are charged by the same potential V, the ratio of the energy stored in the two, would be (E1 refers to capacitor (I) and E2 to capacitor (II)):
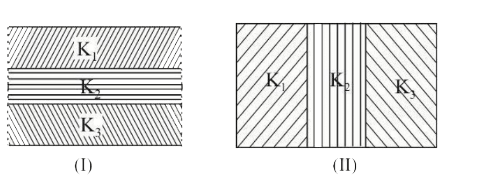
E1E2=(K1+K2+K3)(K2K3+K3K1+K1K2)9K1K2K3
E1E2=K1K2K3(K1+K2+K3)(K2K3+K3K1+K1K2)
E1E2=9K1K2K3(K1+K2+K3)(K2K3+K3K1+K1K2)
E1E2=(K1+K2+K3)(K2K3+K3K1+K1K2)K1K2K3
The correct Answer is:C
E1=12C1V2,E2=12C2V2
1C1=d/3K1∈0A+d/3K2CoA+d/3K3∈0A,C1=3∈0Ad(k1k2k3k1k2+k2k3+k3k4)
C2=A3∈0d(k1+k2+k3) ∴E1E2=C1C2=9k1k2k3(k1+k2+K3)(k1k2+k3−k2+k3k1).
Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 2
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 3
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - LEVEL 2
40 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
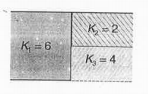
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

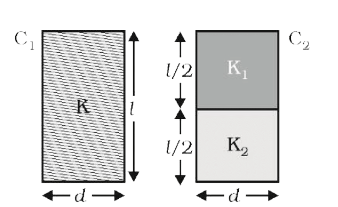
View SolutionTwo identical parallel plate (air) capacitors c1andc2 have capacitances C each. The space between their plates is now filled with dielectrics as shown. If two capacitors still have equal capacitance, obtain the relation betweenn dielectric constants k,k1andk2.
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
View SolutionA parallel plate capacitor of capacitance C (without dielectric) is filled by dielectric slabs as shown in figure. Then the new capacitance of the capacitor is
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
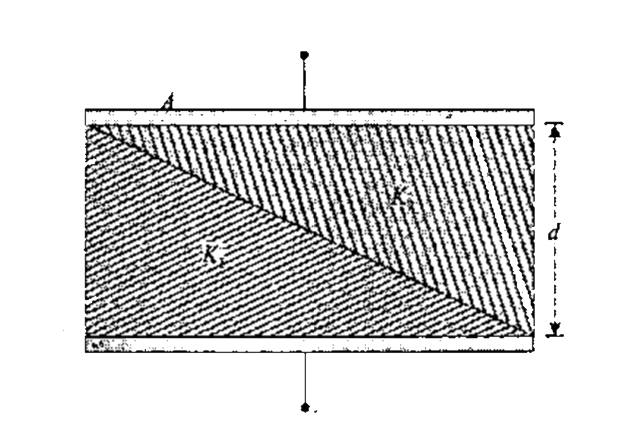
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.

View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View Solution
