The capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
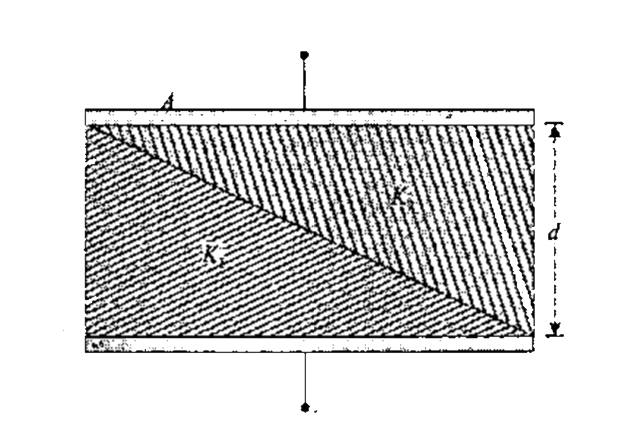
(CK1K2K2−K11nK2K1,) let length of breath of the capacitor be /and b respectively and be the distance between the plates as shown figures then, consider a strip at a distance x if widh dx.
Now, QR=xtanθandPQ=d−xtanθ
Where tanθ=d/1, capacitor of PQ
C1=K1ε0(bdx)d−xtanθ=K1ε0(bdx)d−xd1
C1=K1εb/dxd(1−x)=K1ε0A(dx)d(1−x)andC1=capicitor of QR=K2ε0b(dx)xtanθ
C1=K2ε0A(dx)xd(tanθ=d1)
Now C1 and C2 are in series.Therefore,their resultant capacity C0 will be given by 1C0=1C1+1C2
Then 1C0=1C2+1C2=d(1−x)K1ε0A(dx)+xdK2ε0A(dx)1c0=dε0A(dx)(1−xK1+xk2)=d{K2(1−x)+K1x}ε0AK1K2(dx)
C0=ε0AK1K2D{K2(1−x)+K1x}dx,C0=ε0AK1K2d{K2I+(K1=K2)x}dx
Now, the net capacitance of the given parallel plate capacitor is obtained by adding such infinitesimal capacitors placed parallel from x=0 to x=1
i.e., Finally we get Cn=K1K2A(K2_K1)dln(K2)K1=CK1K2K2−K1ln(K2)kK1, where C=ε0Ad.

Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 46
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 47
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 44
1 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
Find out the capacitance of parallel plate capacitor of plate area A and plate separation d.
View SolutionA parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.

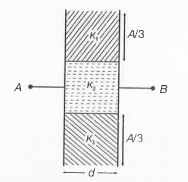
View SolutionA parallel plate capacitor of plate area A and separation d filled with three dielectric materials as show in figure. The dielectric constants are K1, K2 and K3 respectively. The capacitance across AB will be :
View SolutionTo reduce the capacitance of parallel plate capacitor, the space between the plate is
View SolutionA parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness d2 and dielectric constants ∈1 and ∈2 respectively. The equivalent capacitance will be

View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View SolutionA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
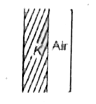
View SolutionAn air capacitor of capacitance C plate area A and plate separation d has been filled with three dielectrics of constant k1=3,k2=6 and k3=4 as shown in figure . What is the new capacitance ?

View SolutionThe capacitance of a parallel plate capacitor is 12μF. If the distance between the plates is doubled and area is halved, then new capacitance will be
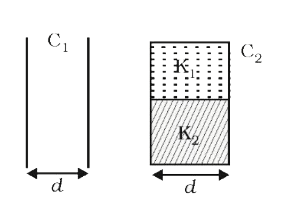
View SolutionYou are given an air filled parallel plate capacitor c1. The space between its plates is now filled with slabs of dielectric constant k1andk2 as shown in c2. Find the capacitances of the capacitor c2 if area of the plates is A distance between the plates is d.
View Solution
