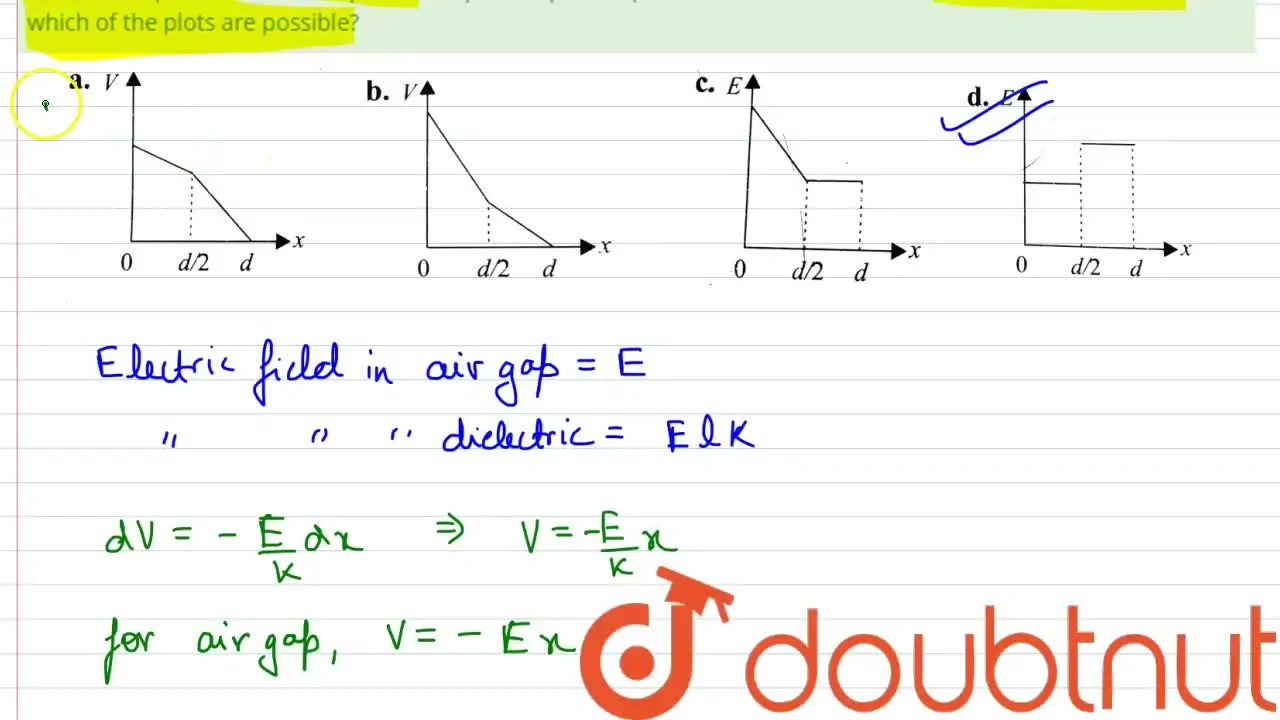
Half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
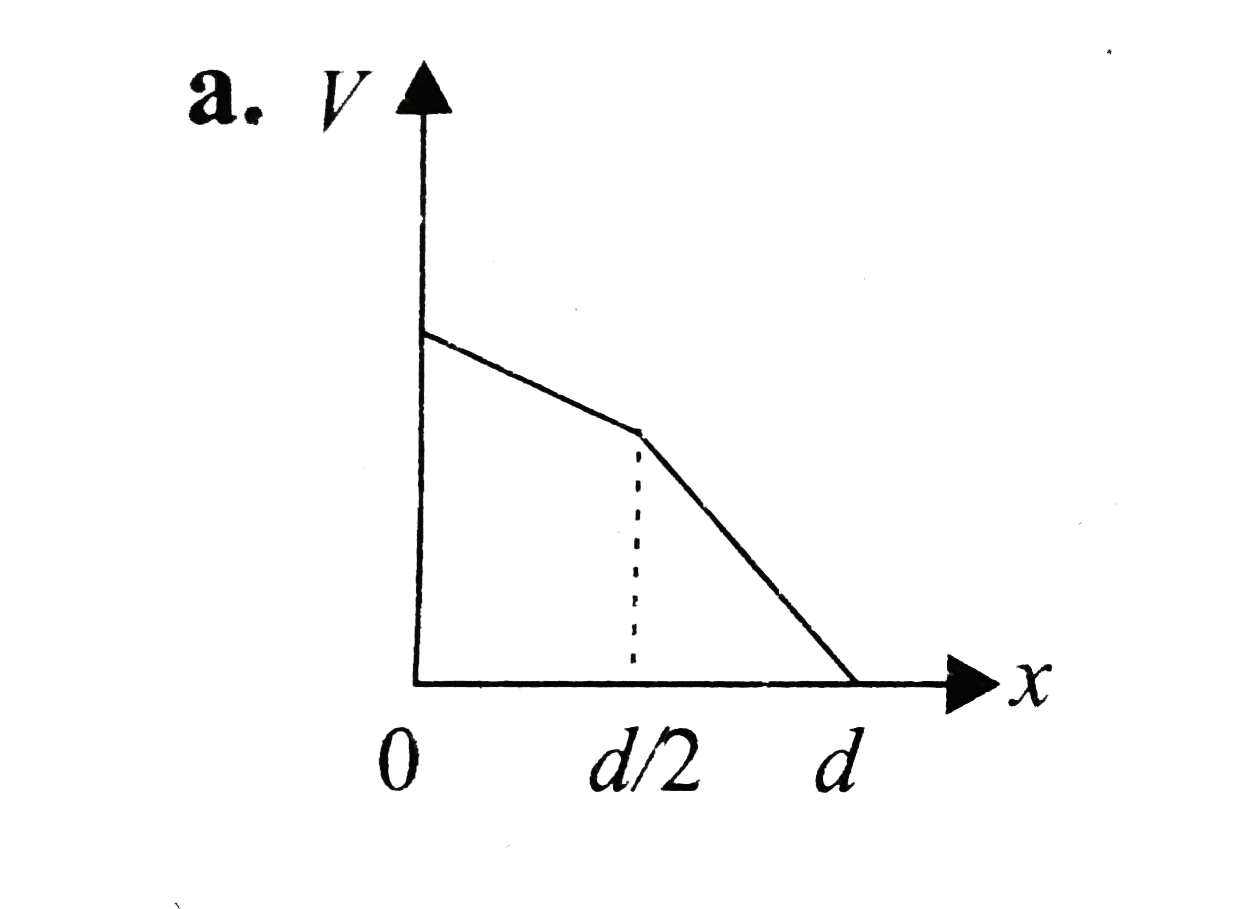
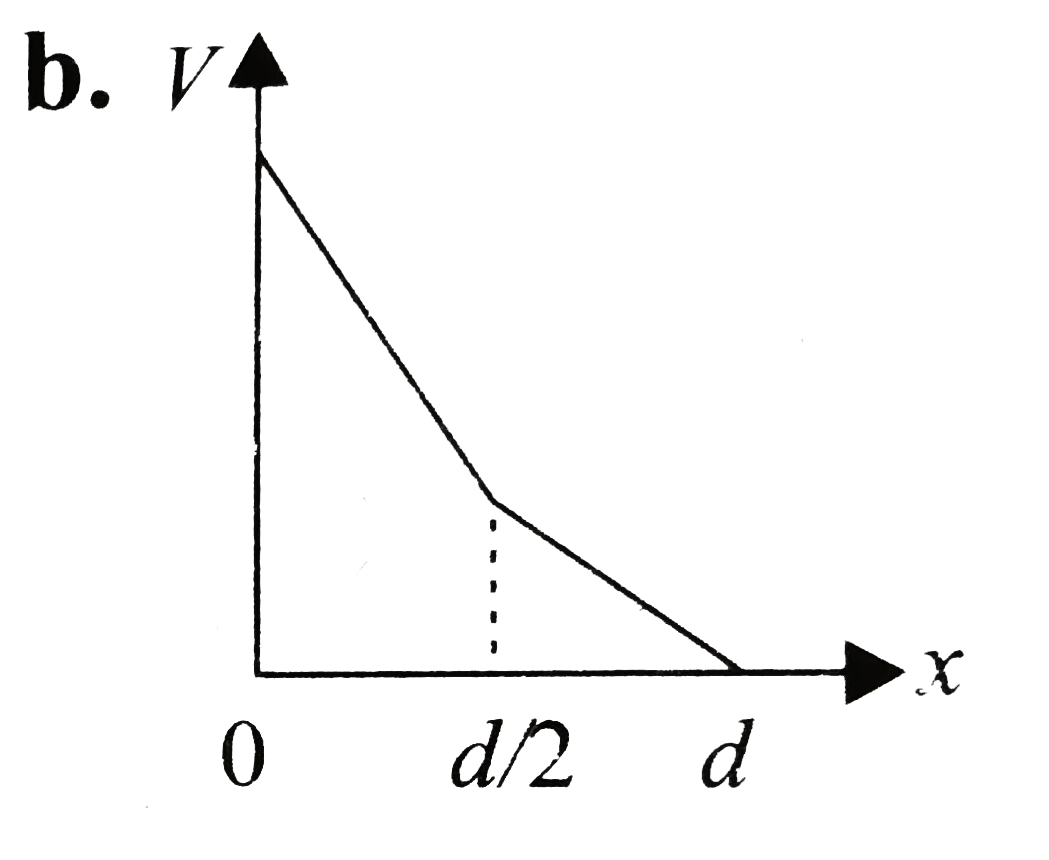

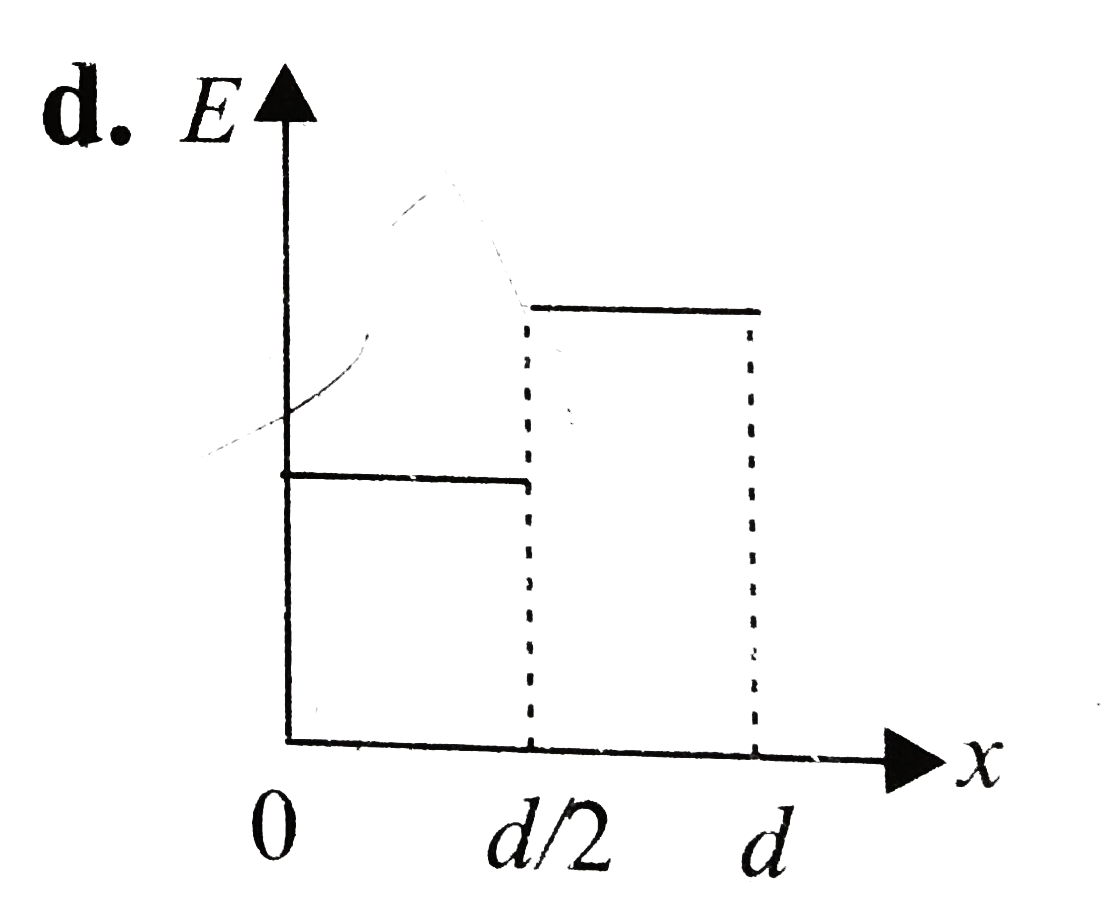
The correct Answer is:A, D
a.,d.
Suppose field in air gap is E. Then in dielectric it is ElK. For dielectric medium
dV=−EKdx or V=EKx
For air gap medium , V=−Ex.
Similar Questions
Parallel Plate Capacitors with and without Dielectric
View SolutionA parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionSpace between the plates of a parallel plate capacitor is filled with a dielectric whose dielectric constant varies with distance as per the relation: K(X)=K0+λX,
(λ= constant, K0= constant, X is perpendicular distance from one plate to a point inside dielectric). The capacitance C1 of this capacitor, would be related to its vacuum capacitance C0 per the relation (d = plate separation):View SolutionA parallel plate capacitar, of capacitance, 20μF, is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
View SolutionThe space between the plates of a parallel plate capacitor of capacitance C is filled with three dielectric slabs of identical size as shown in figure. If the dielectric constants of the three slabs are K1,K2andK3 find the new capacitance.
 View Solution
View SolutionThe space between the plates of a parallel plate capacitor is completely filled with a material of resistivity 2×1011Ωm and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the plates is 20μF. Find the leakage current if a potential difference 2500V is applied across the capacitor.
View SolutionThe space between plates of a parallel plate capacitor is filled by a dielectric and it is charged and then battery is removed. Now dielectric slab is slowly drawn out of the capacitor parallel to the plates. The variation of the potential of capacitor with respect to the length of the dielectric plate drawn out is
View SolutionConsider a parallel plate capacitor. When half of the space between the plates is filled with some dielectric material of dielectric constant K as Shown in Fig. (1) below, the capacitance is C1 . However , if the same dielectric material fills half the space as shown as shown in Fig. (2), the capacitance is C2. Therefore, the ratio C1:C2is
 View Solution
View SolutionThe space between the plates orf a parallel plate capacitor is completely filled with a meterail of resistaivity 2×1011Ωm and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the paltes is 20uF. Find the leakage current if a potential difference 2500 V is applied across the capacitor.
View Solution