Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
To solve the problem of finding the equivalent capacitance of two parallel plate capacitors connected in series, where one capacitor has a dielectric material, we can follow these steps:
Step 1: Identify the given values
- Capacitance of both capacitors without dielectric, C1=C2=40μF
- Dielectric constant for the dielectric material, K=4
Step 2: Calculate the capacitance of the capacitor with the dielectric
The capacitance of a capacitor with a dielectric is given by the formula:
C=C0×K
where C0 is the original capacitance and K is the dielectric constant.
For the second capacitor (which has the dielectric):
C2=C0×K=40μF×4=160μF
Step 3: Write the formulas for capacitors in series
When capacitors are connected in series, the equivalent capacitance Ceq can be calculated using the formula:
1Ceq=1C1+1C2
Step 4: Substitute the values into the series formula
Substituting the values of C1 and C2:
1Ceq=140μF+1160μF
Step 5: Calculate the individual fractions
Finding a common denominator (which is 160):
1Ceq=4160+1160=4+1160=5160
Step 6: Find the equivalent capacitance
Taking the reciprocal to find Ceq:
Ceq=1605=32μF
Final Answer
The equivalent capacitance of the system is:
Ceq=32μF
---
- Capacitance of both capacitors without dielectric, C1=C2=40μF
- Dielectric constant for the dielectric material, K=4
The capacitance of a capacitor with a dielectric is given by the formula:
C=C0×K
where C0 is the original capacitance and K is the dielectric constant.
C2=C0×K=40μF×4=160μF
When capacitors are connected in series, the equivalent capacitance Ceq can be calculated using the formula:
1Ceq=1C1+1C2
Substituting the values of C1 and C2:
1Ceq=140μF+1160μF
Finding a common denominator (which is 160):
1Ceq=4160+1160=4+1160=5160
Taking the reciprocal to find Ceq:
Ceq=1605=32μF
The equivalent capacitance of the system is:
Ceq=32μF
Topper's Solved these Questions
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:worked out examples
Explore 23 Videos
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:Objective 1
Explore 12 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBook:HC VERMA ENGLISHChapter:BOHR'S MODEL AND PHYSICS OF THE ATOMExercise:Short Answer
Explore 10 Videos
- DISPERSION AND SPECTRABook:HC VERMA ENGLISHChapter:DISPERSION AND SPECTRAExercise:Question for short Answer
Explore 6 Videos
Similar Questions
A parallel plate capacitor of capacitance 10μF is connected across a battery of emf 5 mV. Now, the space between the plates of the capacitors is filled with a deielectric material of dielectric constant K=5. Then, the charge that will flow through the battery till equilibrium is reached is
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionFind the capacitance of a capacitor in which the space between the plates is partly filled with a dielectric (Fig. 25.5)

View SolutionA parallel plate capacitar, of capacitance, 20μF, is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionConsider a parallel plate capacitor of 10μF (micro-farad) with air filled in the gap between the plates. Now one half of the space between the plates is filled with a dielectric of dielectric constant 4, as shown in the figure. The capacity of the capacitor charges to

View SolutionThe figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.

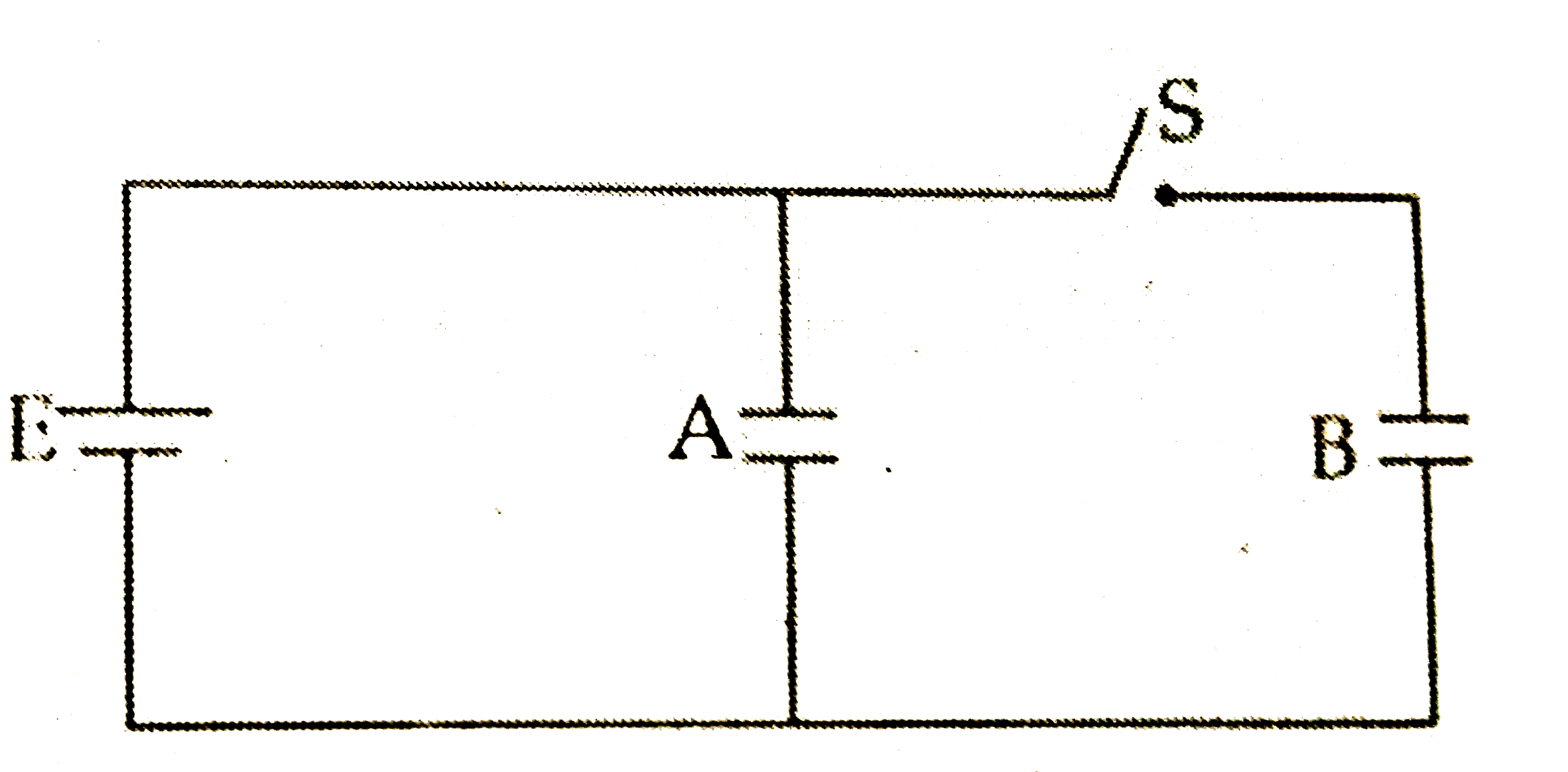
View SolutionTwo identical parallel plate capacitors A and B are
connected to a battery of V volts with the switch S
closed . The switch is now opend and the free
space between the plantes of the capacitors is filled
with a dielectric of dielectric constant K. Find the
rario of the total electrostatic energy stored in both
capacitors before and after the introduction of the dielectric.
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionConsider a disconnected plate capacitor of capacity 10μF with air filled in the gap between the plates. Now one-half of the space between the plates is filled with a dielectric of dielectric constant 4 as shown in .The capacity of the capacitor changes to
 .
.
View Solution

