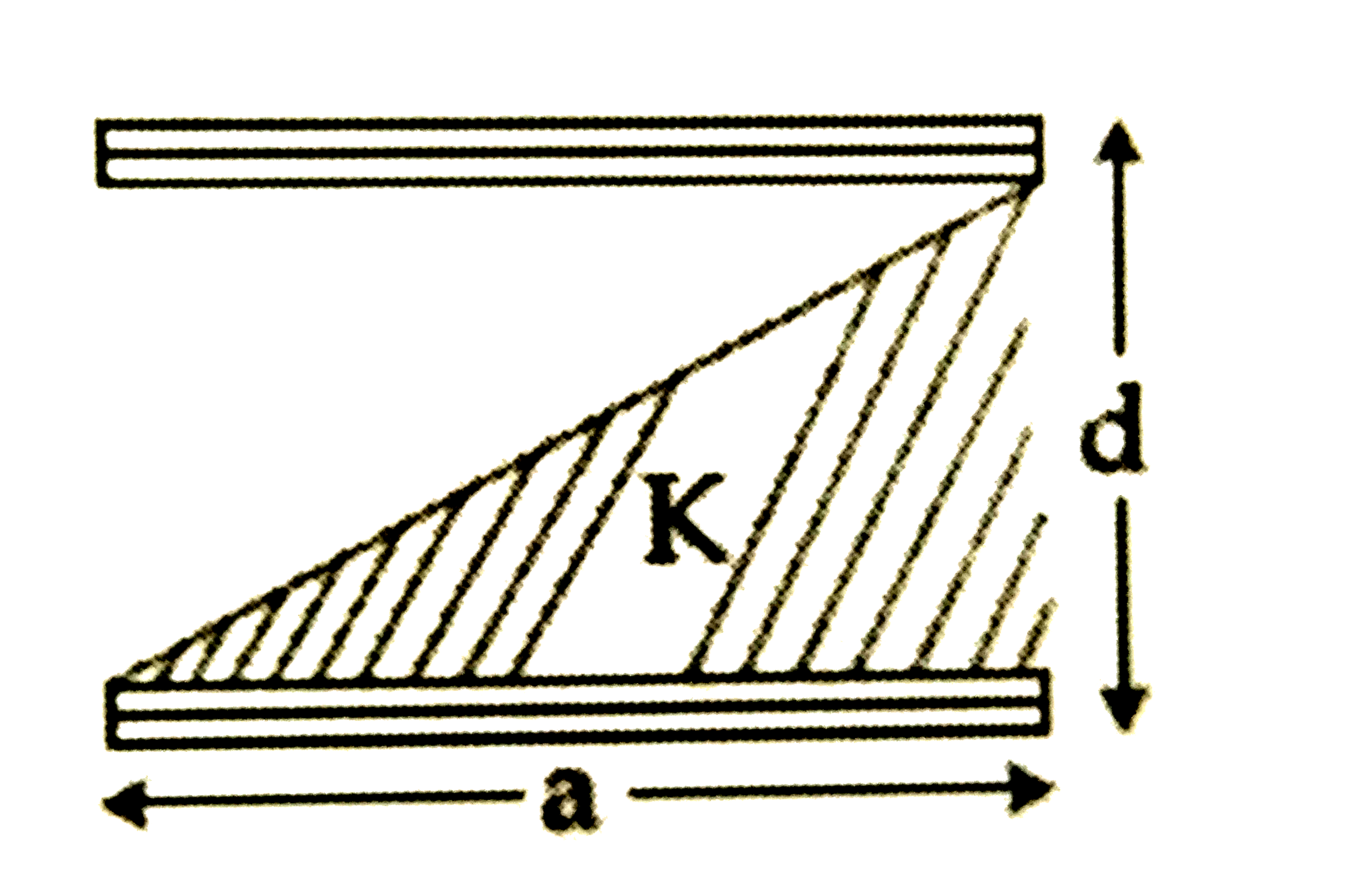
A parallel plate capacitor is made of two square plates of side 'a' , separated by a distance d much less than a. The lower triangular portion is filled with a dielectric of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
 a) K∈0a22d(K+1)
b) K∈0a2d(K−1)InK
c) K∈0a2dInK
d) 12K∈0a2d
a) K∈0a22d(K+1)
b) K∈0a2d(K−1)InK
c) K∈0a2dInK
d) 12K∈0a2d
12K∈0a2d
K∈0a2dlnK
K∈0a2d(K−1)lnK
K∈0a42d(K+1)
The correct Answer is:C
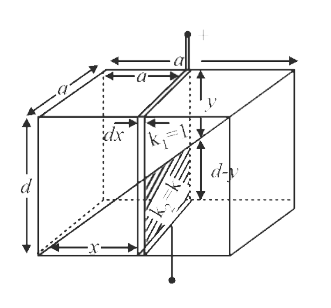
For vacuum k1=1
For dielectric k2=k
Consider two elemental slabs (one in vacuum and other in dielectric) having capacitances dC1&dC2,dC1anddC2 are in series.
1dC=1dC1+1dC2=y∈0k1adx+d−y∈0k2adx,dC=Capacitance of composite elemental slabs.
⇒1dC=k2+y+(d−y)k1∈0k1k2adx=ky+d−y∈0kadx
All such dC's are in parallel ∴Total capacitance, C=∫dC=∈0ka∫dxky+d−y . . (i)
Now, d−yx=da⇒x=(d−y)ad . . (ii) , from equation (i) & (ii)
C=∈0ka[ad]∫−d0dy(k−1)y+d=∈0ka2dln[(k−1)y+d]d0(k−1),C=∈0ka2dlnk(k−1) i.e., option (C).
Topper's Solved these Questions
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Advance ( Archive ) LEVEL 2
Explore 1 Video
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Advance ( Archive ) LEVEL 3
Explore 1 Video
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:LEVEL 2
Explore 40 Videos
- BASIC MATHEMATICS & VECTORSBook:VMC MODULES ENGLISHChapter:BASIC MATHEMATICS & VECTORSExercise:Impeccable
Explore 50 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
Similar Questions
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then

View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View SolutionA capacitor is formed by two square metal-plates of edge a, separated by a distance d. Dielectrics of dielectric constants K1andK2 are filled in the gap as shown in fig. Find the capacitance.

View SolutionAir filled capacitor of capacitance 2μF is filled with three dielectric material of dielectric constant K1=4,K2=4 and K3=6 as shown in the figure . The new capacitance of the capacitor is
View SolutionA parallel plate capacitor has plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as k(x)=K(1+ax) where ‘x’ is shown in figure. If (al)<<1 , the total capacitance of the system is best given by the expression:

View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
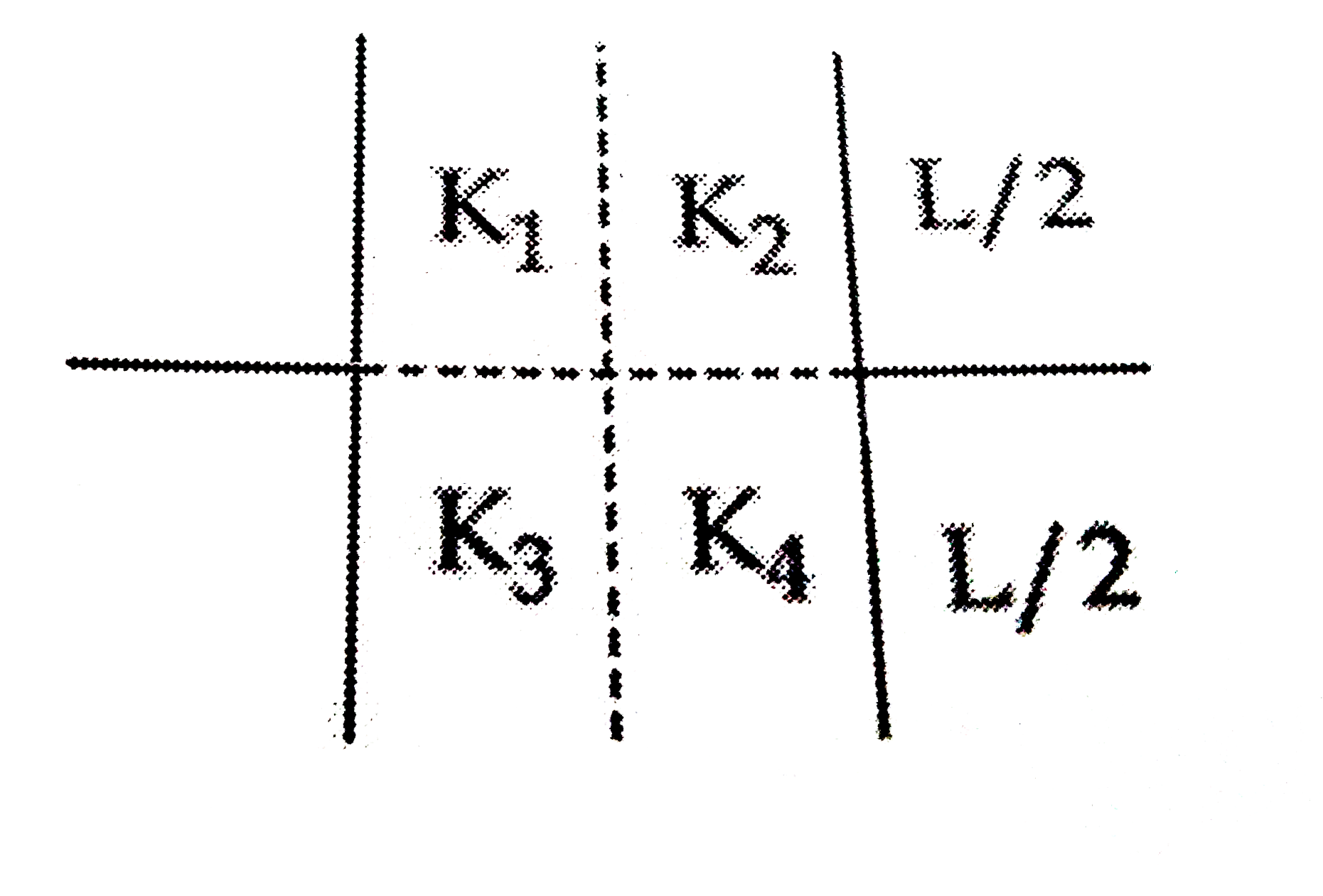
View Solution
