A block of mass m is pushed up against a spring, compressing it a distance x, and the block is then released. The spring projects the block along a frictionaless horizontal surface, grving the block a speed v. The same spring projects a second block of mass 4m, giving it a speed 3v. What distance was the spring compressed in the second case ?
6x
x/6
36x
12x
The correct Answer is:A
To solve the problem, we need to apply the principles of energy conservation and the relationship between the spring's compression and the kinetic energy imparted to the blocks.
1. Initial Setup:
- Let the spring constant be k.
- When the first block of mass m is compressed by a distance x, the potential energy stored in the spring is given by:
PE=12kx2
- This potential energy is converted into kinetic energy when the block is released, giving it a speed v:
KE=12mv2
2. Energy Conservation for the First Block:
- Setting the potential energy equal to the kinetic energy, we have:
12kx2=12mv2
- Simplifying this gives:
kx2=mv2(Equation 1)
3. Setup for the Second Block:
- Now, consider the second block of mass 4m which is projected with a speed 3v.
- The potential energy stored in the spring when compressed by a distance y is:
PE2=12ky2
- The kinetic energy of the second block when it is projected is:
KE2=12(4m)(3v)2=12(4m)(9v2)=18mv2
4. Energy Conservation for the Second Block:
- Setting the potential energy equal to the kinetic energy for the second block gives:
12ky2=18mv2
- Simplifying this gives:
ky2=36mv2(Equation 2)
5. Relating the Two Equations:
- From Equation 1, we have kx2=mv2.
- We can express v2 from this equation:
v2=kx2m
- Substitute v2 into Equation 2:
ky2=36m(kx2m)
- This simplifies to:
ky2=36kx2
- Dividing both sides by k (assuming k≠0):
y2=36x2
- Taking the square root of both sides gives:
y=6x
Final Answer:
The distance the spring was compressed in the second case is y=6x.
- Let the spring constant be k.
- When the first block of mass m is compressed by a distance x, the potential energy stored in the spring is given by:
PE=12kx2
- This potential energy is converted into kinetic energy when the block is released, giving it a speed v:
KE=12mv2
- Setting the potential energy equal to the kinetic energy, we have:
12kx2=12mv2
- Simplifying this gives:
kx2=mv2(Equation 1)
- Now, consider the second block of mass 4m which is projected with a speed 3v.
- The potential energy stored in the spring when compressed by a distance y is:
PE2=12ky2
- The kinetic energy of the second block when it is projected is:
KE2=12(4m)(3v)2=12(4m)(9v2)=18mv2
- Setting the potential energy equal to the kinetic energy for the second block gives:
12ky2=18mv2
- Simplifying this gives:
ky2=36mv2(Equation 2)
- From Equation 1, we have kx2=mv2.
- We can express v2 from this equation:
v2=kx2m
- Substitute v2 into Equation 2:
ky2=36m(kx2m)
- This simplifies to:
ky2=36kx2
- Dividing both sides by k (assuming k≠0):
y2=36x2
- Taking the square root of both sides gives:
y=6x
The distance the spring was compressed in the second case is y=6x.
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2 PARAGRAPH QUESTIONS
Explore 2 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE MAIN (ARCHIVE)
Explore 53 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
A block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m moving at a speed 'v' compresses as spring through a distance 'x' before its speed is halved. Find the spring constant of the spring.
View SolutionThe spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
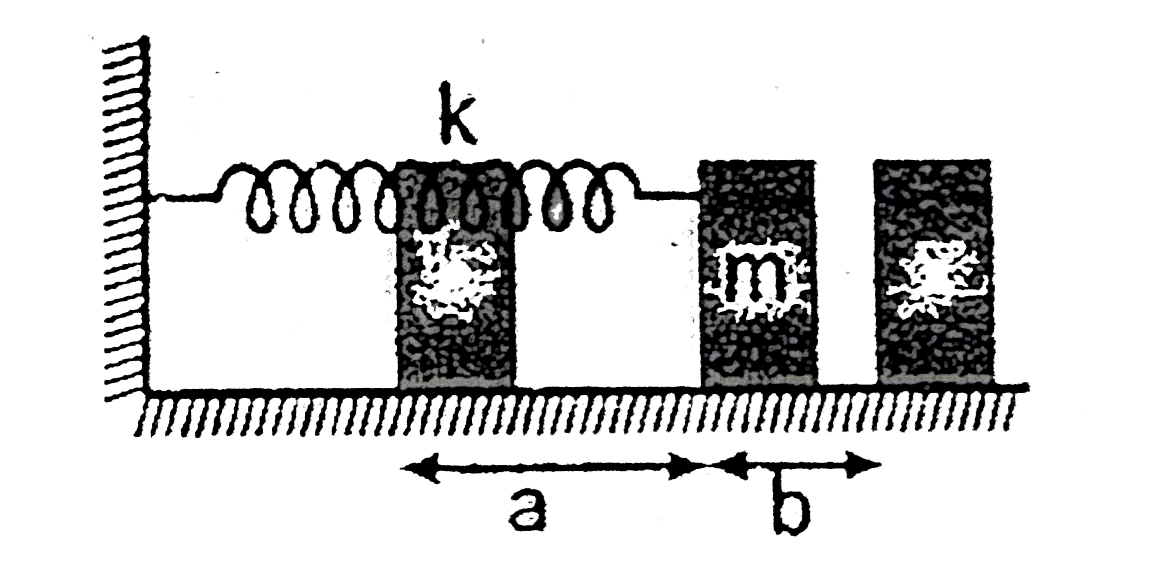
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is

View SolutionA block of mass m moving at a speed v compresses a spring through a distance x before its speed is halved. The spring constant of the spring is 6mv2nx2. Find value of n.
View SolutionA small block of mass 500 gm is pressed against a horizontal spring fixed at one end to a distance of 10 cm. when released, the block moves horizontally till it leaves the spring. Where it will hit the ground 5 m below the spring. (Take k = 100 N/m of spring)
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

View Solution