An object of mass 5 kg is projected with a velocity of at an angle of to the horizontal. At the highest point of its path, the projectile explodes and breaks up into two fragments of masses 1 kg and 4 kg. The fragments separate horizontally after the explosion, which releases internal energy such that K.E. of the system at the highest point is doubled Find the separation between the two fragments when they reach the ground.
The correct Answer is:5
The height of
At the highest point the projectile explodes and breaks into two particles which separate horizontally. As there is no external force acting in horizontal direction, hence linear momentum in horizontal direction should be conserved just before and just after explosion.
Applying conservation of linear momentum
The kinetic energy at the highest point initially
The kinetic energy after collision
After solving (i) and (ii) we get
Taking the pair .
The relative velocity of separation of fragments in horizontal direction,
Let the time taken by each fragment to reach the ground be t
Using
Hence the separation between the fragments when they reach the ground
.
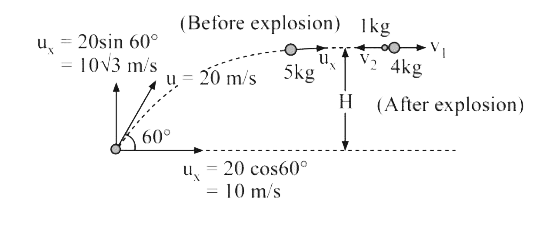
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2 PARAGRAPH QUESTIONS
Explore 2 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE MAIN (ARCHIVE)
Explore 53 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
A body of mass 2 kg is projected at 20 ms−1 at an angle 60∘above the horizontal. Power due to the gravitational force at its highest point is
View SolutionA body of mass 1kg is projected with velocity 50ms−1 at an angle of 30∘ with the horizontal. At the highest point of its path a force 10 N starts acting on body for 5s vertically upward besids gravitational force, what is horizontal range of the body (Take, g=10ms−2)
View Solution
Knowledge Check
An object of mass 5 kg is projecte with a velocity of 20ms−1 at an angle of 60∘ to the horizontal. At the highest point of its path , the projectile explodes and breaks up into two fragments of masses 1kg and 4 kg. The fragments separate horizontally after the explosion, which releases internal energy such that K.E. of the system at the highest point is doubled. Calculate the separation betweent the two fragments when they reach the ground.
A11 mB22 mC44 mD66 m
A particle of mass m is projected with a velocity v at an angle of θ with horizontal. The angular momentum of the particle at the highest point of its trajectory is equal to :
View SolutionA projectile is fired with velocity.v0 at an angle 60∘ with horizontal . At top of its trajectory it explodes into two fragments of equal mass. If one fragment retraces the path then the speed of the other fragment is
View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View SolutionA stationary body explodes into two fragments of masses m1 and m2. If momentum of one fragment is p, the energy of explosion is
View SolutionA stationary body explodes into two fragments of masses m1 and m2. If momentum of one fragment is p, the energy of explosion is
View SolutionA projectile of mass 3kg is projected with velocity 50m/s at 37∘ from horizontal. After 2s, explosion takes place and the projectile breaks into two parts of masses 1kg and 2kg. The first part comes to rest just after explosion.
Find,
(a) the velocity of second part just after explosion.
(b) maximum height attained by this part. Take g=10m/s2
View SolutionA ball is projected with 20√2m/s at angle 45∘ with horizontal.The angular velocity of the particle at highest point of its journey about point of projection is
View Solution

