Two identical balls are dropped from the same height onto a hard surface, the second ball being released exactly when the first ball bollides with the surface. If the first ball has made two more collisions by the time the second one collides. Then the coefficient of restitution between the ball and the surface satisfies :
e>0.5
e=0.5
e=√3−12
e<√3−12
The correct Answer is:D
To solve the problem, we need to analyze the motion of the two balls and the collisions they undergo. Here’s a step-by-step breakdown of the solution:
Step 1: Determine the time taken by the first ball to hit the ground
When the first ball is dropped from a height h, we can use the second equation of motion to find the time t0 it takes to hit the ground. The equation is:
h=12gt20
Rearranging gives:
t0=√2hg
Step 2: Calculate the velocity of the first ball just before impact
Using the third equation of motion, we can find the velocity v0 of the first ball just before it strikes the ground:
v0=√2gh
Step 3: Analyze the first collision
Upon colliding with the ground, the first ball will rebound with a velocity reduced by the coefficient of restitution e:
v1=ev0=e√2gh
Step 4: Determine the time taken for the first ball to collide again
The time taken for the first ball to rise back to the maximum height and fall again can be calculated. The time to rise to the maximum height is given by:
tup=v1g=e√2ghg
The time to fall back down from that height is the same, so the total time for the first collision and return is:
t1=2⋅tup=2⋅e√2hg
Step 5: Analyze the second collision
After the first collision, the ball will again collide with the ground. The velocity just before the second collision will be:
v2=ev1=e2v0=e2√2gh
The time taken for the ball to rise and fall again is:
tdown=2⋅v2g=2⋅e2√2hg
Step 6: Total time for two collisions
The total time taken for the first ball to collide twice is:
ttotal=t1+t2=2⋅e√2hg+2⋅e2√2hg
Factoring out the common terms gives:
ttotal=2√2hg(e+e2)
Step 7: Set up the inequality
According to the problem, the time taken for the second ball to hit the ground t0 must be less than the total time for the first ball to collide twice:
t0<ttotal
Substituting the expressions we derived:
√2hg<2√2hg(e+e2)
Step 8: Simplifying the inequality
Dividing both sides by √2hg:
1<2(e+e2)
Rearranging gives:
2e2+2e−1>0
Step 9: Solving the quadratic inequality
To find the roots of the quadratic equation 2e2+2e−1=0:
Using the quadratic formula:
e=−b±√b2−4ac2a=−2±√(2)2−4⋅2⋅(−1)2⋅2
Calculating gives:
e=−2±√4+84=−2±√124=−2±2√34=−1±√32
Step 10: Determine the valid range for e
Since e must be positive, we take the positive root:
e<−1+√32
Conclusion
The coefficient of restitution e must satisfy:
e<−1+√32
When the first ball is dropped from a height h, we can use the second equation of motion to find the time t0 it takes to hit the ground. The equation is:
Using the third equation of motion, we can find the velocity v0 of the first ball just before it strikes the ground:
Upon colliding with the ground, the first ball will rebound with a velocity reduced by the coefficient of restitution e:
The time taken for the first ball to rise back to the maximum height and fall again can be calculated. The time to rise to the maximum height is given by:
After the first collision, the ball will again collide with the ground. The velocity just before the second collision will be:
The total time taken for the first ball to collide twice is:
According to the problem, the time taken for the second ball to hit the ground t0 must be less than the total time for the first ball to collide twice:
Dividing both sides by √2hg:
To find the roots of the quadratic equation 2e2+2e−1=0:
Since e must be positive, we take the positive root:
The coefficient of restitution e must satisfy:
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2 PARAGRAPH QUESTIONS
Explore 2 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE MAIN (ARCHIVE)
Explore 53 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
Ball 1 collides directly with another identical ball 2 at rest. Velocity of second ball becomes two times that of 1 after collison. Find the coefficient of restitution between the two balls?
View SolutionBall 1 collides directly with another identical ball 2 at rest. Velocity of second ball becomes two times that of 1 after collison. Find the coefficient of restitution between the two balls?
View Solution
Knowledge Check
A ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
Ae2hBeh2Ce4hDhe4
A ball is dropped on a horizontal surface from height h. If it rebounds upto height h2 after first collision then coefficient of restitution between ball and surface is
View SolutionA ball of mass m collides with the ground at an angle. With the vertical. If the collision lasts for time t, the average force exerted by the ground on the ball is : (e = coefficient of restitution between the ball and the ground)
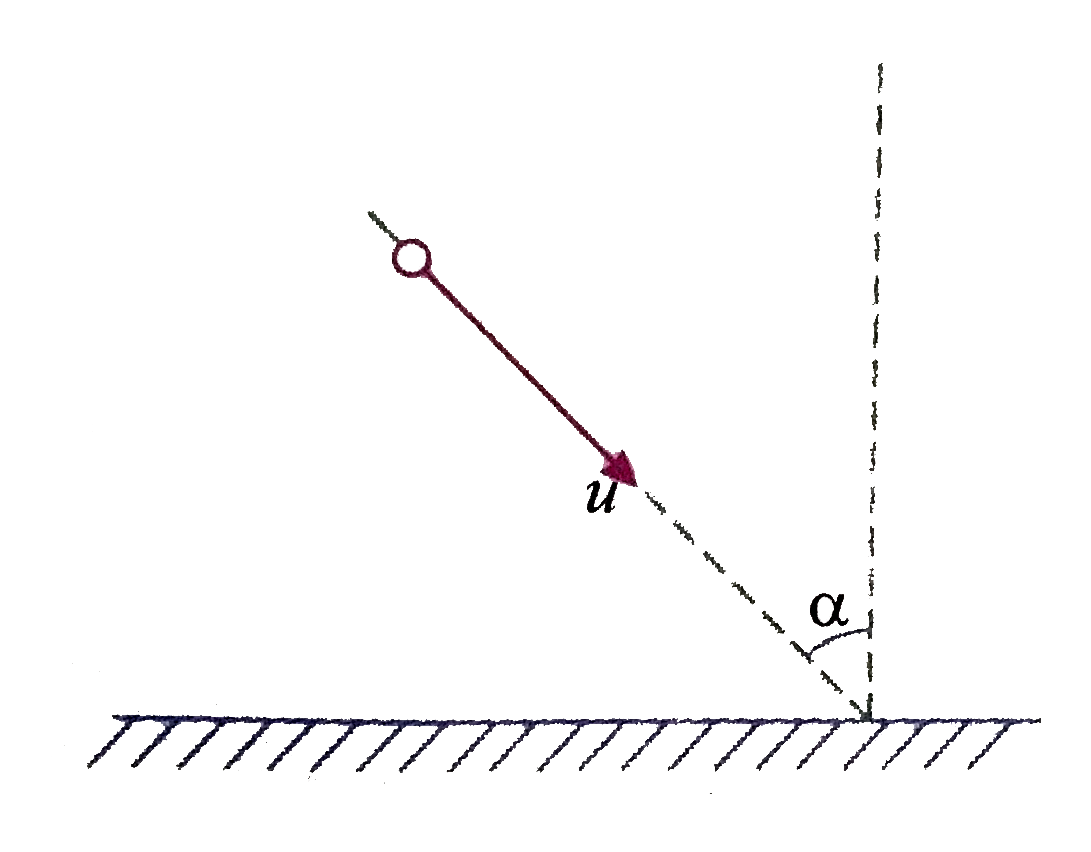 .
.
View SolutionA ball is dropped from height 5m. The time after which ball stops rebounding if coefficient of restitution between ball and ground e=1/2, is
View SolutionA ball is dropped from height 'H' onto a horizontal surface. If the coefficient of restitution is 'e' then the total time after which it comes to rest is
View SolutionA ball is dropped from height 'H' onto a horizontal surface. If the coefficient of restitution is 'e' then the total time after which it comes to rest is
View SolutionA ball is dropped from a height of 20 m in the floor and rebounds to 1.25 m after second collision, then coefficient of restitution e is
View SolutionA small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
View Solution

