A small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
SHM
periodic but not SHM
not periodic
SHM for half a period and non-periodic for rest half of the period
The correct Answer is:B
To solve the problem, we need to analyze the motion of a small ball dropped into a non-viscous liquid with a density less than that of the ball. Here’s a step-by-step breakdown of the reasoning:
Step 1: Understand the Forces Acting on the Ball
When the ball is dropped into the liquid, two main forces act on it:
- The gravitational force (weight) acting downwards: Fg=mg
- The buoyant force acting upwards, which can be calculated using Archimedes' principle: Fb=ρl⋅V⋅g
Where:
- m is the mass of the ball
- g is the acceleration due to gravity
- ρl is the density of the liquid
- V is the volume of the ball
Step 2: Compare the Densities
Given that the density of the liquid (ρl) is less than the density of the ball (ρs), we can conclude:
- The weight of the ball is greater than the buoyant force: mg>ρl⋅V⋅g
Step 3: Determine the Net Force
Since the weight of the ball is greater than the buoyant force, the net force acting on the ball when it is submerged is:
Fnet=mg−ρl⋅V⋅g
This net force acts downwards.
Step 4: Analyze the Motion
As the ball moves through the liquid, it will continue to accelerate downwards until it reaches the bottom of the container or until it comes to rest at the surface, depending on the depth of the liquid. Since the net force is not proportional to the displacement from an equilibrium position, the motion cannot be classified as Simple Harmonic Motion (SHM).
Step 5: Determine if the Motion is Periodic
Although the motion is not SHM, we can analyze whether it is periodic. The ball will oscillate up and down around a mean position (the surface of the liquid) as it bobs up and down due to the balance of forces. Since it takes the same time to return to a position after being displaced, we can classify the motion as periodic.
Conclusion
The motion of the ball is periodic but not Simple Harmonic Motion (SHM).
Final Answer
The motion of the ball is periodic but not SHM.
---
When the ball is dropped into the liquid, two main forces act on it:
- The gravitational force (weight) acting downwards: Fg=mg
- The buoyant force acting upwards, which can be calculated using Archimedes' principle: Fb=ρl⋅V⋅g
- m is the mass of the ball
- g is the acceleration due to gravity
- ρl is the density of the liquid
- V is the volume of the ball
Given that the density of the liquid (ρl) is less than the density of the ball (ρs), we can conclude:
- The weight of the ball is greater than the buoyant force: mg>ρl⋅V⋅g
Since the weight of the ball is greater than the buoyant force, the net force acting on the ball when it is submerged is:
Fnet=mg−ρl⋅V⋅g
This net force acts downwards.
As the ball moves through the liquid, it will continue to accelerate downwards until it reaches the bottom of the container or until it comes to rest at the surface, depending on the depth of the liquid. Since the net force is not proportional to the displacement from an equilibrium position, the motion cannot be classified as Simple Harmonic Motion (SHM).
Although the motion is not SHM, we can analyze whether it is periodic. The ball will oscillate up and down around a mean position (the surface of the liquid) as it bobs up and down due to the balance of forces. Since it takes the same time to return to a position after being displaced, we can classify the motion as periodic.
The motion of the ball is periodic but not Simple Harmonic Motion (SHM).
The motion of the ball is periodic but not SHM.
Similar Questions
Knowledge Check
A ball is dropped from a height h on the ground If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
Ahe2nBhenCe2nhDhe2nA ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
Ae2hBeh2Ce4hDhe4
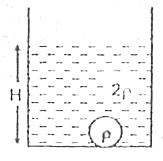
A small ball of density ρ is placed from the bottom of a tank in which a non viscous liquid of density 2ρ is filled . Find the time taken by the ball to reach the surface of liquid and maximum height reached above the bottom of container . (Size of the ball and any type of drag force acting on the ball are negligible )
View SolutionAssertion: A ball is dropped from a certain height above the free suface of and ideal fluid. When the ball enters the liquid it mau accelerate or retard.
Reason: Ball accelerates of retards it all depends on the dinsity of ball and the density of liquid.

View SolutionA ball rises to the surface of a liquid with constant velocity. The density of the liquid is four time the density of the material of the ball. The frictional force of the liquid on the rising ball is greater than the weight of the ball by a factor of
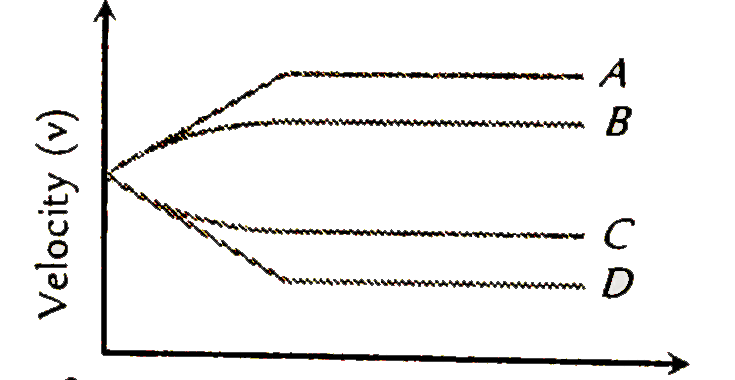
View SolutionA small spherical solid ball is dropped from a great height in a viscous liquid. Its journey in the liquid is best described in the diagram given below by the
View SolutionA ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
View SolutionA ball rises to the surface of a liquid with constant velocity. The density of the liquid is four lime the density of the material of the ball. The frictional force of the liquid on the rising ball is greater than the weight of the ball by a factor of
View Solution

