A small ball of density is placed from the bottom of a tank in which a non viscous liquid of density is filled . Find the time taken by the ball to reach the surface of liquid and maximum height reached above the bottom of container . (Size of the ball and any type of drag force acting on the ball are negligible )
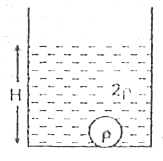
Acceleration of ball = where & W are force of buoyancy & weight of the body respectively .
Now
Velocity at surface
Now maximum height above bottom
Similar Questions
A ball of density ρ is dropped from a height on the surface of a non-viscous liquid of density 2ρ. Choose the correct options.

View SolutionIf liquid of density ρ is filled in an open cylindrical container to height h, then pressure at bottom
View SolutionA small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
View SolutionA ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
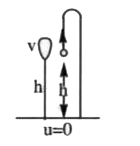
View SolutionA balloon starts from rest from the ground and moves with uniform acceleration g/8. When it reaches a height h a ball is dropped from it. Find the time taken by the ball to reach the ground.
View SolutionA non viscous liquid of density ρ is filled in a tube with A as the area of cross section, as shown in the figure. If the liquid is slightly depressed in one of the arms, the liquid column oscillates with a frequency

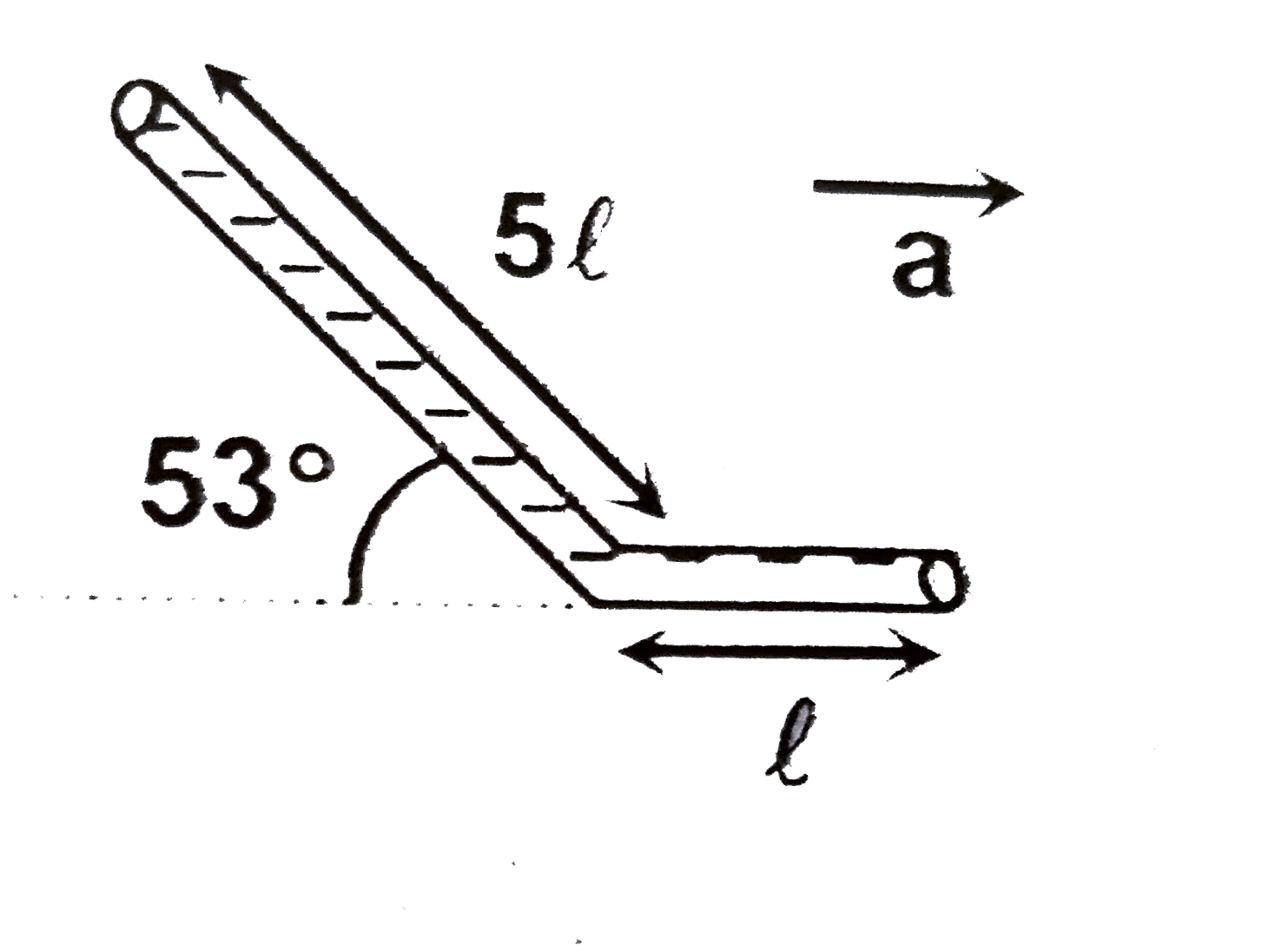
View SolutionIn the given tube liquid density ρ is filled. Find the acceleration of the tuve towards right direction such that no liquid will fall out of the tube.
View SolutionA small ball of density rho_(0) is released from the surface of a liquid whose density varies with depth h as ρ=ρ02(α+βh). Mass of the ball is m. Select the most appropriate one option.
View SolutionAssertion : A ball is released from the bottom of a tank filled with a liquid. It moves upwards . In moving upwards upthrust will decrease.
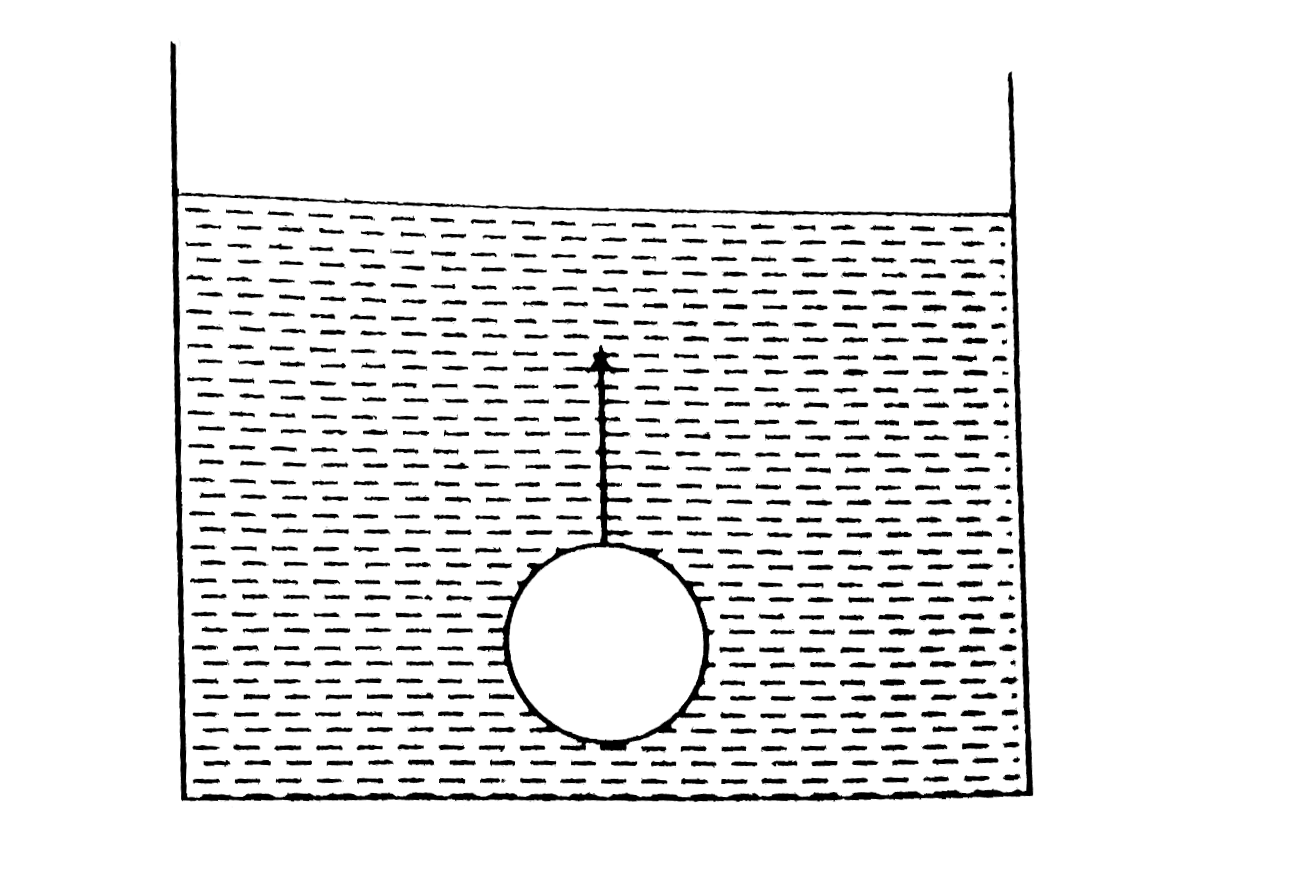
Reason : Density of ball is less than the density of liquid.
View SolutionA small ball of density ρ is immersed in a liquid of density σ(>ρ) to a depth h and released. The height above the surface of water up to which the ball will jump is
View Solution
