Question

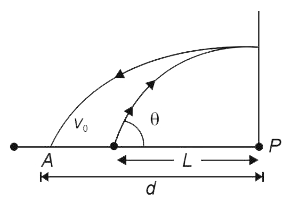
A ball is projected at ${\displaystyle t=0}$ with velocity ${\displaystyle v_0}$ at angle ${\displaystyle \theta }$ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :

Options

A. (a)Ball will return to ground at `t = (2v_0 sin theta)/(g)`
B. (b)`d = e(R - L) ("where" R "is" (v_0 sin 2theta)/(g))`
C. (c)maximum height during motion `= (v_0^2 sin^2 theta)/(2g)`
D. (d)it will return to ground at `t lt (2v_0 sin theta)/(g)`

Answer

A::B::C

Explanation

`v_(_|_) = v_0 sin theta` does not suffer change due to collision.
So time of flight and maximum height which depend on vertical velocity does not change.
`v_(||) = v_0 cos theta` (before collision)
`v_(||("after collision")) = ev_0 cos theta`
Time taken to reach ground after collision
`t' = (2 v_0 sin theta)/(g) " ":. " " d = ev_(0) cos theta xx t' = e(R - L)`