A mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
2v√3
v√3
v
√3v
The correct Answer is:A
To solve the problem, we need to analyze the momentum before and after the collision. Here’s a step-by-step solution:
Step 1: Define the initial momentum
The first mass m is moving with a velocity v along the x-axis. Therefore, the initial momentum →pinitial of the system can be expressed as:
→pinitial=m→v=mv^i
where ^i is the unit vector in the x-direction.
Step 2: Define the final momentum of the first mass
After the collision, the first mass moves with a velocity of v√3 in the y-direction. Thus, the final momentum →p1 of the first mass is:
→p1=m(v√3^j)
where ^j is the unit vector in the y-direction.
Step 3: Define the final momentum of the second mass
Let the velocity of the second mass after the collision be →v2. The momentum of the second mass →p2 can be expressed as:
→p2=m→v2
Step 4: Apply conservation of momentum
Since the collision is inelastic and there are no external forces acting on the system, the total initial momentum must equal the total final momentum:
→pinitial=→p1+→p2
Substituting the expressions we have:
mv^i=m(v√3^j)+m→v2
Step 5: Cancel the mass m
We can divide the entire equation by m (assuming m≠0):
v^i=v√3^j+→v2
Step 6: Rearranging to find →v2
Rearranging the equation gives us:
→v2=v^i−v√3^j
Step 7: Calculate the magnitude of →v2
To find the speed of the second mass, we need to calculate the magnitude of →v2:
|→v2|=
⎷(v)2+(−v√3)2
Calculating the second term:
(−v√3)2=v23
Thus,
|→v2|=√v2+v23=√3v23+v23=√4v23=2v√3
Final Answer
The speed of the second mass after the collision is:
2v√3
The first mass m is moving with a velocity v along the x-axis. Therefore, the initial momentum →pinitial of the system can be expressed as:
→pinitial=m→v=mv^i
where ^i is the unit vector in the x-direction.
After the collision, the first mass moves with a velocity of v√3 in the y-direction. Thus, the final momentum →p1 of the first mass is:
→p1=m(v√3^j)
where ^j is the unit vector in the y-direction.
Let the velocity of the second mass after the collision be →v2. The momentum of the second mass →p2 can be expressed as:
→p2=m→v2
Since the collision is inelastic and there are no external forces acting on the system, the total initial momentum must equal the total final momentum:
→pinitial=→p1+→p2
Substituting the expressions we have:
mv^i=m(v√3^j)+m→v2
We can divide the entire equation by m (assuming m≠0):
v^i=v√3^j+→v2
Rearranging the equation gives us:
→v2=v^i−v√3^j
To find the speed of the second mass, we need to calculate the magnitude of →v2:
|→v2|=
⎷(v)2+(−v√3)2
Calculating the second term:
(−v√3)2=v23
Thus,
|→v2|=√v2+v23=√3v23+v23=√4v23=2v√3
The speed of the second mass after the collision is:
2v√3
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2 PARAGRAPH QUESTIONS
Explore 2 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE MAIN (ARCHIVE)
Explore 53 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
A sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View Solution
Knowledge Check
A body of mass m, moving with velocity μ collides elasticity with another body at rest having mass M. If the body of mass M moves with velocity V, then the velocity of the body of mass m after the impact is
Am−Mm+MμBm−Mm+MVCm+MVm+MDmu−MVm
A ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View SolutionA body of mass m2 moving with velocity v0 collides elastically with another mass of m3 . Find % change in KE of first body
View SolutionTwo spherical balls of masses m1 and m2 collide as shown in figure. After collision mass m1 moves with velocity u/3 in a direction perpendicular to original direction. The angle θ at which mass m2 will move after collision is
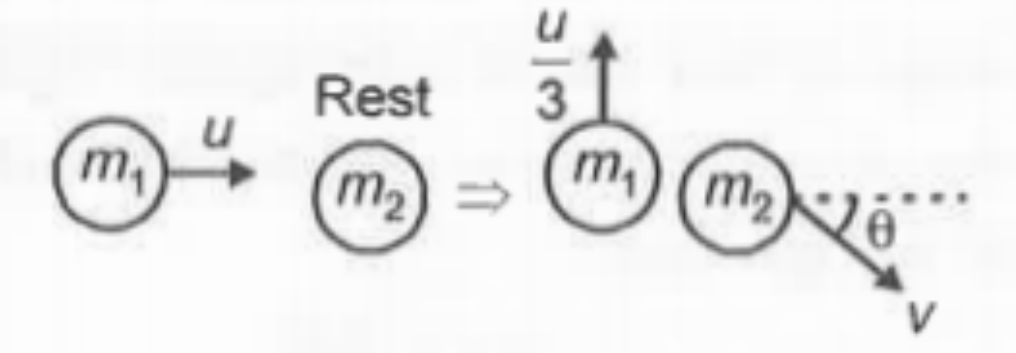
View SolutionTwo spherical balls of masses m1 and m2 collide as shown in figure. After collision mass m1 moves with velocity u/3 in a direction perpendicular to original direction. The angle θ at which mass m2 will move after collision is
View SolutionOn a friction surface a block a mass M moving at speed v collides elastic with another block of same mass M which is initially at rest . After collision the first block moves at an angle θ to its initial direction and has a speed v3. The second block's speed after the collision is
View SolutionTwo sphere AandB of masses m1andm2 respectivelly colides. A is at rest initally and B is moving with velocity v along x-axis. After collision B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
View SolutionTwo spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision, B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction
View Solution