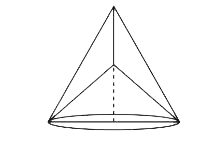
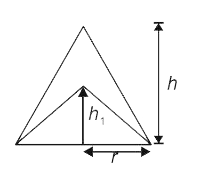
A uniform solid right circular cone has its base cut out in conical shape shown in figure such that the hollow portion is a right circular cone on the same base. Find what should be the height of the hollow portion so that the centre of mass of the remaining portion may coincide with the vertex of the hollow portion.
h3
h4
2h3
h6
The correct Answer is:A
M=ρ13πr2h,YCM=h4 [Before removed)
M=ρ13πr2h1,Y1CM=h14 [For removed part)
YCM=h1=MY−M1Y1M−M1
=ρ13πr2(h24−h214)ρ13πr2(h−h1)⇒h1=h1+h4⇒h1=h3
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2 PARAGRAPH QUESTIONS
Explore 2 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE MAIN (ARCHIVE)
Explore 53 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
Knowledge Check
If a right circular cone has a lateral surface area of 6π and a slant height of 6, what is the radius of the base ?
A0.50B0.75C1.00D1.25A right circular cone has a volume of 24π cubic inches. If the height of the cone is 2 inches, what is the radius, in inches, of the base of the cone?
A2√3B6C12D36
The base radii of two right circular cones of the same height are in the ratio 3:5. Find the ratio of their volumes.
View SolutionA right circular cone is 3.6 cm high and radius of its base is 1.6 cm. It is melted and recast into a right circular cone with radius of its base as 1.2 cm. Find its height.
View SolutionA right circular cone is 3.6 cm high and radius of its base is 1.6 cm. It is melted and recast into a right circular cone with radius of its base as 1.2 cm. Find its height.
View SolutionA right circular cone is 3.6 cm high and radius of its base is 1.6 cm. It is melted and recast into a right circular cone with radius of its base as 1.2 cm. Find its height.
View SolutionA right circular cone is 3.6 cm high and radius of its base is 1.6 cm. It is melted and recast into a right circular cone with radius of its base as 1.2 cm. Find its height.
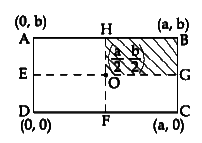
View SolutionA uniform rectangular thin sheet ABCD of mass M has length a and breadth b, as shown in the figure. If the shaded portion HBGO is cut-off, the coordinates of the center of mass of the remaining portion will be:
View Solution

