Acceleration of a particle is given by
a = 2x
(i) It’s velocity at position x. Given that v = 10 m/s when x = 0.
(ii) Minimum speed that the particle can attain
To solve the problem step by step, we will follow the given information and use the principles of kinematics.
Step 1: Understand the relationship between acceleration, velocity, and position
We are given the acceleration of a particle as:
a=2x
We know that acceleration can also be expressed in terms of velocity and position:
a=vdvdx
Step 2: Set up the equation
Equating the two expressions for acceleration, we have:
vdvdx=2x
Now, we can rearrange this to separate variables:
vdv=2xdx
Step 3: Integrate both sides
Next, we integrate both sides. The left side will be integrated with respect to v and the right side with respect to x:
∫vdv=∫2xdx
This gives us:
v22=x2+C
where C is the constant of integration.
Step 4: Apply initial conditions
We are given that the velocity v=10m/s when x=0. We can use this information to find the constant C:
(10)22=(0)2+C⟹50=C
So, the equation becomes:
v22=x2+50
Step 5: Solve for velocity v
Now, we can solve for v:
v2=2x2+100
Taking the square root gives:
v=√2x2+100
Step 6: Find the minimum speed
To find the minimum speed, we need to analyze the expression v=√2x2+100. The minimum value occurs when x=0:
vmin=√2(0)2+100=√100=10m/s
Final Answers
(i) The velocity at position x is given by:
v=√2x2+100
(ii) The minimum speed that the particle can attain is:
vmin=10m/s
---
We are given the acceleration of a particle as:
a=2x
We know that acceleration can also be expressed in terms of velocity and position:
a=vdvdx
Equating the two expressions for acceleration, we have:
vdvdx=2x
Now, we can rearrange this to separate variables:
vdv=2xdx
Next, we integrate both sides. The left side will be integrated with respect to v and the right side with respect to x:
∫vdv=∫2xdx
This gives us:
v22=x2+C
where C is the constant of integration.
We are given that the velocity v=10m/s when x=0. We can use this information to find the constant C:
(10)22=(0)2+C⟹50=C
So, the equation becomes:
v22=x2+50
Now, we can solve for v:
v2=2x2+100
Taking the square root gives:
v=√2x2+100
To find the minimum speed, we need to analyze the expression v=√2x2+100. The minimum value occurs when x=0:
vmin=√2(0)2+100=√100=10m/s
(i) The velocity at position x is given by:
v=√2x2+100
vmin=10m/s
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:LEVEL 1
Explore 75 Videos
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:LEVEL 2
Explore 65 Videos
- JEE MAIN REVISON TEST-23Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISON TEST-23Exercise:PHYSICS (SECTION 2)
Explore 1 Video
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
Similar Questions
Acceleration of a particle is given by
a=1/V
Where V is the velocity . Find
(i) Velocity of particle at time t, given that v = 10 m/s at t = 0.
(ii) Velocity of particle when its position is x, given that speed is 3 m/s at x = 0.
View SolutionAcceleration of a particle is given by
a=3t2+2t+1
Where t is time . Find
(i) its velocity at time t assuming velocity to be 10 m/s at t = 0.
(ii) its position at time t assuming that the particle is at origin at t = 0.
(iii) What is the average speed of the particle in the duration t = 0 to t = 1s?
(iv) What is the average acceleration of the particle in the duration t = 0 to t = 1s?
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View SolutionThe acceleration of a particle is given by a (t)=(3.00 m/s2−(2.00ms3))t. (a) Find the initial speed v0 such that the particle will have the same x -coordinate at t =5.00 as it had at t=0. (b)What will be the velocity at t =5.00s?
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View SolutionAcceleration of a particle is increasing linearly with time. Its acceleration is 10 m/s2att=0and20m/s2att=5s.Also, its speed is 5m/s at t =0 and its positions is x= -100m at t =0 .Find at time t its acceleration ,velocity and positions.
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View SolutionThe figure shows the force (F) versus displacement (s) graph for a particle of mass m=2kg initially at rest.
(i) The maximum speed of the particle occurs at x = …..m
(ii) The maximum speed of the particle is ….ms−1
(iii) The particle once again has its speed zero at x =....m
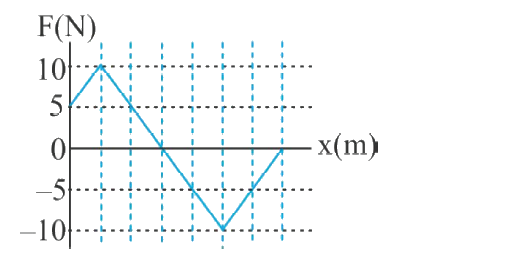
View SolutionA particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
View Solution