Question

A particles is moving eastwards with a velocity of $5m{s}^{-1}$. In 10 s, the velocity changes to $5m{s}^{-1}$ northwards. The average acceleration in this time is

Options

A. zero
B. ` 1//sqrt 2ms^(-2) ` towards north-west
C. `1//2 ms^(-2) ` towards north -west
D. ` 1//2 ms^(-2) ` towards north

Answer

B

Explanation

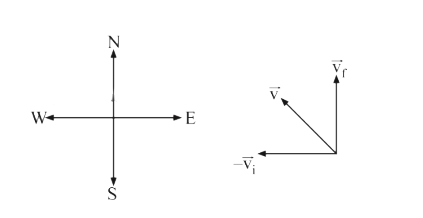
Average acceleration
` overset-a _(av) =(oversetto v_(f) -oversetto v_i)/( t) =(oversetto v_f+(-overset to v_i) )/(t ) =(oversetto v)/(t) `
To find the resultant of ` oversetto v _f and -oversetto v _f ` we draw the following figure.
` |oversetto v | =sqrt( v_f^(2) +v_1^(2) )= sqrt( 5^(2)+ 5^(2))= 5 sqrt 2ms^(-1) `
Since , ` " " |oversettov _f) =|-oversetto v_i) |`
` overset to v ` in directed in between `oversetto v_f and -oversetto v_i`
Therefore, is directed towards ` N-overset-W rArr " " overset to a_(av) =(5sqrt 2))/(10) =(1)/(sqrt2) `