A river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
The direction of boat's velocity is 30∘ west of north.
The direction of boat's velocity is north - west.
Resultant velocity is 5√3ms−1.
Resultant velocity of boat is 5√2ms−1.
The correct Answer is:A, C
To solve the problem of a boat crossing a river with a current, we can break down the steps as follows:
Step 1: Understand the Problem
The river flows with a velocity Vr=5m/s and the boat has a velocity Vb=10m/s. The boat is crossing the river by the shortest path, which means it is moving perpendicular to the riverbank.
Step 2: Visualize the Motion
We can visualize the situation as a right triangle where:
- The horizontal leg represents the velocity of the river (Vr).
- The vertical leg represents the component of the boat's velocity that is perpendicular to the riverbank.
- The hypotenuse represents the boat's actual velocity (Vb).
Step 3: Set Up the Relationship
Since the boat is crossing the river by the shortest path, it must have a component of its velocity that counters the river's current. We can use trigonometric functions to relate these velocities.
Step 4: Use the Sine Function
Using the sine function, we can express the relationship as follows:
sin(θ)=VrVb
Substituting the values:
sin(θ)=510=12
Step 5: Calculate the Angle
To find the angle θ:
θ=arcsin(12)=30∘
This angle is measured from the direction of the river's flow towards the direction of the boat's motion, which is 30 degrees west of north.
Step 6: Find the Resultant Velocity
To find the resultant velocity of the boat with respect to the river, we can use the Pythagorean theorem:
Vresultant=√V2b−V2r
Substituting the values:
Vresultant=√102−52=√100−25=√75=5√3m/s
Conclusion
The boat crosses the river at an angle of 30 degrees west of north, and its resultant velocity with respect to the river is 5√3m/s.
---
The river flows with a velocity Vr=5m/s and the boat has a velocity Vb=10m/s. The boat is crossing the river by the shortest path, which means it is moving perpendicular to the riverbank.
We can visualize the situation as a right triangle where:
- The horizontal leg represents the velocity of the river (Vr).
- The vertical leg represents the component of the boat's velocity that is perpendicular to the riverbank.
- The hypotenuse represents the boat's actual velocity (Vb).
Since the boat is crossing the river by the shortest path, it must have a component of its velocity that counters the river's current. We can use trigonometric functions to relate these velocities.
Using the sine function, we can express the relationship as follows:
sin(θ)=VrVb
Substituting the values:
sin(θ)=510=12
To find the angle θ:
θ=arcsin(12)=30∘
This angle is measured from the direction of the river's flow towards the direction of the boat's motion, which is 30 degrees west of north.
To find the resultant velocity of the boat with respect to the river, we can use the Pythagorean theorem:
Vresultant=√V2b−V2r
Substituting the values:
Vresultant=√102−52=√100−25=√75=5√3m/s
The boat crosses the river at an angle of 30 degrees west of north, and its resultant velocity with respect to the river is 5√3m/s.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Assertion - Reasoning
Explore 5 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Comprehension
Explore 21 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Single Correct
Explore 76 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
A river is flowing with a velocity of 2m/s. If the width of river in 100 m and swimmer wants to cross river is shortest time, what time (in sec) would he take if velocity of swimmer in still water is 4 m/s ?
View SolutionVelocity of boat in still water is 13 m/s. If water flows ina river with a velocity of 5 m/s. What is the difference in times taken by him to cross the river in the shortest path and in the shortest time. If the width of the river is 10 m.
View SolutionThe velocity of a boat in still water is 10 m/s. If water flows in the river with a velocity of 6 m/s what is the difference in times taken to cross the river in the shortest path and the shortest time. The width of the river is 80 m.
View SolutionWidth of a river is 30m, velocity is 4m/s and rowing velocity is 5m/s
(a) Make the velocity diagram for crossing the river in shortest time. Then, find this shortest time, net velocity of boatman and drigt along the river.
(b) Can the boatman reach a point just oppsite on the other shore? If yes then make the velocity diagram, the direction in which the should row his boat and the time taken to cross the river in this case.
(c) How long will it iake hom to row 10m up the stream and then back to his starting point?
View SolutionA 400m wide river is flowing at a rate of 2.0ms−1. A boat is sailing with a velocity of 10ms−1 with respect to the water, in a direction perpendicular to the river.
(a) Find the time taken by the boat to reach the opposite bank.
(b) How far from the point directly opposite to the starting point does the boat reach the opposite bank ?
( c) In what direction does the boat actually move ?
View Solution2 km wide river flowing with a rate of 5 km/hr. A man can swim in the still water with10 km/hr. He wants to cross the river along shortest path find
Crossing time
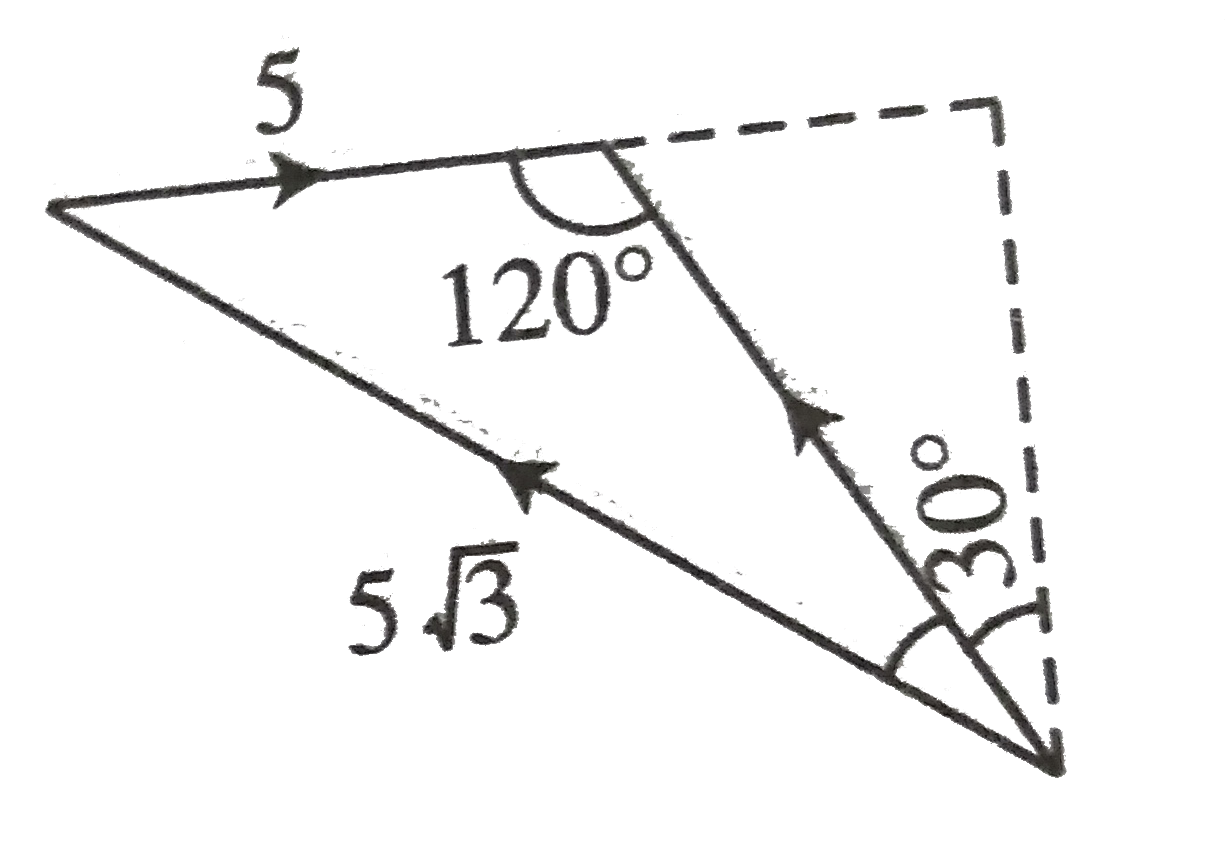
View SolutionA motor boat is to reach at a point 30∘ upstream on the outer side of a river flowing with velocity 5ms−1. The velocity of motor boat with respect to water is 5(√3)ms−1. The driver should steer the boat at an angle.
View SolutionAt a harbour, a boat is standing and wind is blowing at a speed of √2m/sec. due to which , the flag on the boat flutters along north− east. Now the boat enters in to river, which is flowing with a velocity of 2m/sec. Due north. The boat starts with zero velocity relative to the river and its constant acceleration relative to the river is 0.2m/sec2 due east. In which direction will the flag flutter at 10 seconds ?
View SolutionA boat is moving towards east velocity 4 m/s w.r.t still water and river is flowing towards north with velocity 2 m/s and the wind blowing towards north with velocity 6 m/s. the direction of the flag blown over by the wind hpisted on the boat is
View SolutionThe width of river is 1 km. The velocity of boat is 5 km/hr. The boat covered the width of river with shortest will possible path in 15 min. Then the velocity of river stream is:
View Solution