A body is projected with velocity u at an angle of projection θ with the horizontal. The direction of velocity of the body makes angle 30∘ with the horizontal at t=2s and then after 1s it reaches the maximum height. Then
a. u=20√3ms−1,
b. θ=60∘
c. θ=30∘
d. u=10√3ms−1
The correct Answer is:A, B
To solve the problem step by step, we will analyze the projectile motion of the body and derive the required values.
Step 1: Understand the given information
We know that:
- The body is projected with an initial velocity u at an angle θ with the horizontal.
- At t=2 seconds, the direction of the velocity makes an angle of 30∘ with the horizontal.
- After 1 second from that moment (i.e., at t=3 seconds), the body reaches its maximum height.
Step 2: Determine the total time of ascent
Since the body reaches its maximum height at t=3 seconds, the total time of ascent is:
T=3 seconds
Step 3: Relate time of ascent to initial vertical velocity
The time of ascent T is given by the formula:
T=usinθg
where g is the acceleration due to gravity (approximately 10m/s2). Thus, we can write:
3=usinθ10
From this, we can express usinθ:
usinθ=30(Equation 1)
Step 4: Analyze the velocity components at t=2 seconds
At t=2 seconds, the horizontal and vertical components of the velocity can be expressed as:
- Horizontal component Vx=ucosθ
- Vertical component Vy=usinθ−gt
Substituting t=2 seconds into the vertical component:
Vy=usinθ−20(since g≈10 m/s2)
Step 5: Use the angle of velocity at t=2 seconds
Since the angle of the velocity makes 30∘ with the horizontal, we can use the tangent function:
tan(30∘)=VyVx
Given tan(30∘)=1√3, we can write:
VyVx=1√3
Substituting the expressions for Vy and Vx:
usinθ−20ucosθ=1√3
Step 6: Cross-multiply and simplify
Cross-multiplying gives:
√3(usinθ−20)=ucosθ
Expanding this:
√3usinθ−20√3=ucosθ
Rearranging gives us:
√3usinθ−ucosθ=20√3
Factoring out u:
u(√3sinθ−cosθ)=20√3(Equation 2)
Step 7: Solve the equations
Now we have two equations:
1. usinθ=30
2. u(√3sinθ−cosθ)=20√3
Substituting usinθ=30 into Equation 2:
u(√3⋅30u−cosθ)=20√3
This simplifies to:
30√3−ucosθ=20√3
Thus:
ucosθ=10√3
Step 8: Find u and θ
Now we have:
1. usinθ=30
2. ucosθ=10√3
Dividing these two equations:
usinθucosθ=3010√3⟹tanθ=3√3=√3
Thus:
θ=60∘
Step 9: Calculate u
Using usin60∘=30:
u⋅√32=30⟹u=30⋅2√3=20√3
Final Answer
Thus, we find:
- u=20√3
- θ=60∘
We know that:
- The body is projected with an initial velocity u at an angle θ with the horizontal.
- At t=2 seconds, the direction of the velocity makes an angle of 30∘ with the horizontal.
- After 1 second from that moment (i.e., at t=3 seconds), the body reaches its maximum height.
Since the body reaches its maximum height at t=3 seconds, the total time of ascent is:
T=3 seconds
The time of ascent T is given by the formula:
T=usinθg
where g is the acceleration due to gravity (approximately 10m/s2). Thus, we can write:
3=usinθ10
From this, we can express usinθ:
usinθ=30(Equation 1)
At t=2 seconds, the horizontal and vertical components of the velocity can be expressed as:
- Horizontal component Vx=ucosθ
- Vertical component Vy=usinθ−gt
Vy=usinθ−20(since g≈10 m/s2)
Since the angle of the velocity makes 30∘ with the horizontal, we can use the tangent function:
tan(30∘)=VyVx
Given tan(30∘)=1√3, we can write:
VyVx=1√3
Substituting the expressions for Vy and Vx:
usinθ−20ucosθ=1√3
Cross-multiplying gives:
√3(usinθ−20)=ucosθ
Expanding this:
√3usinθ−20√3=ucosθ
Rearranging gives us:
√3usinθ−ucosθ=20√3
Factoring out u:
u(√3sinθ−cosθ)=20√3(Equation 2)
Now we have two equations:
1. usinθ=30
2. u(√3sinθ−cosθ)=20√3
u(√3⋅30u−cosθ)=20√3
This simplifies to:
30√3−ucosθ=20√3
Thus:
ucosθ=10√3
Now we have:
1. usinθ=30
2. ucosθ=10√3
usinθucosθ=3010√3⟹tanθ=3√3=√3
Thus:
θ=60∘
Using usin60∘=30:
u⋅√32=30⟹u=30⋅2√3=20√3
Thus, we find:
- u=20√3
- θ=60∘
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Comprehension
21 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Single Correct
76 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A body is projected with a velocity u at an angle of 60∘ to the horizontal. The time interval after which it will be moving in a direction of 30∘ to the horizontal is
View SolutionA body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA body is projected with velocity 24 ms−1 making an angle 30° with the horizontal. The vertical component of its velocity after 2s is (g=10ms−1 )
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA body is projected with a speed (u) at an angle to the horizontal to have maximum range. What is its velocity at the highest point ?
View SolutionA stone projected with a velocity u at an angle (theta )with the horizontal reaches maximum heights H1. When it is projected with velocity u at an angle (π2−θ) with the horizontal, it reaches maximum height H2. The relations between the horizontal range R of the projectile, H1andH2, is
View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View Solution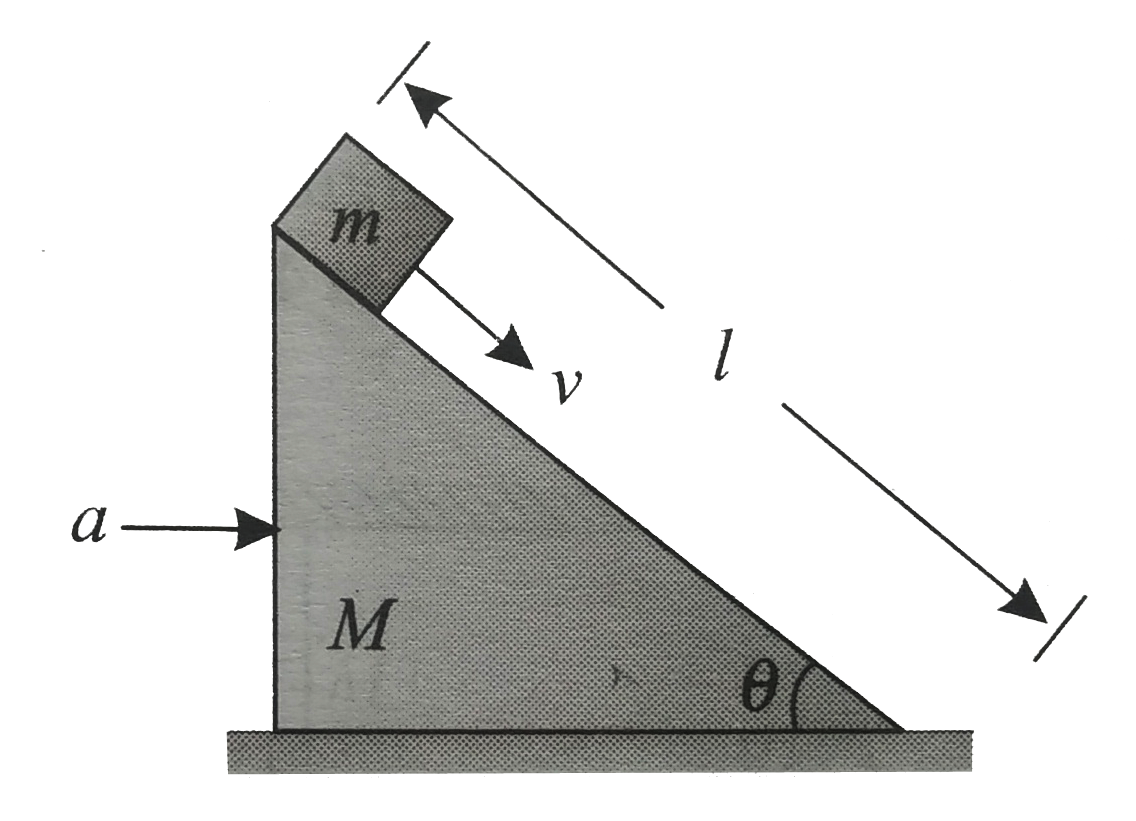
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionA body is projected with velocity u such that in horizontal range and maximum vertical heights are same.The maximum height is
View Solution
