A particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
zero
42 m
Infinite
None of these
The correct Answer is:A
To solve the problem, we need to analyze the motion of the particle given its acceleration function and initial conditions.
1. Understanding the Given Information:
- The acceleration of the particle is given by the equation a=3x−4.
- At time t=0, the particle is at rest at position x=43 m.
- Since the particle is at rest, its initial velocity v0=0.
2. Calculating Initial Acceleration:
- To find the initial acceleration, we substitute the initial position into the acceleration equation:
a(0)=3(43)−4
- Simplifying this:
a(0)=4−4=0
- Therefore, the initial acceleration a(0)=0.
3. Interpreting the Results:
- Since the particle is at rest and has zero acceleration at t=0, it suggests that there is no net force acting on the particle.
- According to Newton's first law, an object at rest will remain at rest unless acted upon by a net external force.
4. Conclusion on Motion:
- Given that both the initial velocity and acceleration are zero, the particle will not start moving.
- Thus, the distance traveled by the particle in any time interval, including 5 seconds, is zero.
5. Final Answer:
- The distance traveled by the particle in 5 seconds is 0 meters.
- The acceleration of the particle is given by the equation a=3x−4.
- At time t=0, the particle is at rest at position x=43 m.
- Since the particle is at rest, its initial velocity v0=0.
- To find the initial acceleration, we substitute the initial position into the acceleration equation:
a(0)=3(43)−4
- Simplifying this:
a(0)=4−4=0
- Therefore, the initial acceleration a(0)=0.
- Since the particle is at rest and has zero acceleration at t=0, it suggests that there is no net force acting on the particle.
- According to Newton's first law, an object at rest will remain at rest unless acted upon by a net external force.
- Given that both the initial velocity and acceleration are zero, the particle will not start moving.
- Thus, the distance traveled by the particle in any time interval, including 5 seconds, is zero.
- The distance traveled by the particle in 5 seconds is 0 meters.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Multiple Correct Answer Type
Explore 26 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Linked Comprehension Type
Explore 35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
A particle is moveint along the x-axis whose instantaneous speed is given by v2=108−9x2. The acceleration of the particle is.
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionA particle is moving along the x-axis whose position is given by x=4−9t+t33. Mark the correct statement(s) in relation to its motion.
View SolutionA particle moves along the X-axis as x=u(t−2s)+a(t−2s)2.
View SolutionPosition of a particle moving along x-axis is given by x=2+8t−4t2. The distance travelled by the particle from t=0 to t=2 is:-
View SolutionA particle is moving along the x-axis with an acceleration a = 2x where a is in ms–2andx is in metre. If the particle starts from rest at x=1 m, find its velocity when it reaches the position x = 3.
View SolutionA particle starts moving in a straight line from rest with an acceleration (inm/s2) given by : a=12√x, where x is the distance travelled by the particle (in meters ) The velocity of the particle at the instant when its acceleration is 48m/s2 is .......m/s
View SolutionA particle is moving on X−axis. Its velocity time graph is given in the figure. Find distance travelled by the particle in 5sec.
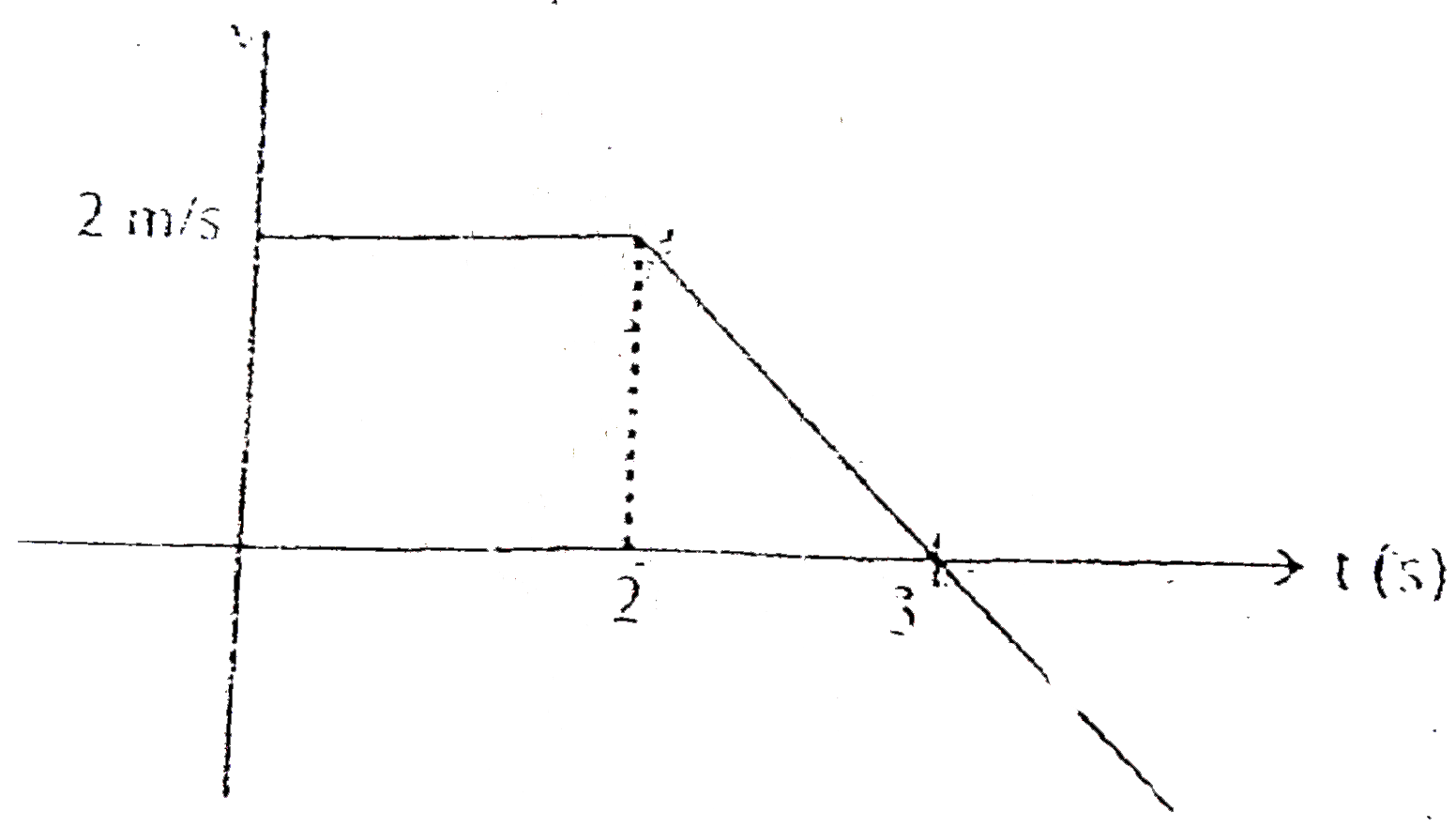
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionVelocity of particle moving along x-axis is given as v=(x3−x2+2) m/sec. Find the acceleration of particle at x=2 meter.
View Solution
